14 Nov 08 Wann benutzt man $$\equiv$$ und wann $$\Leftrightarrow$$?

Bei der Korrektur der Hausaufgaben ist mir aufgefallen, dass viele $$\Leftrightarrow$$ statt $$\equiv$$ benutzen, wenn sie die logische Terme umformen. Die Musterlösungen verwenden immer $$\equiv$$, wie vielleicht aufgefallen ist, und ich habe das Verwenden von $$\Leftrightarrow$$ in der letzten Hausaufgabe auch immer angestrichen (aber keine Punkte abgezogen).
Deshalb ist es sinnvoll, einen kleinen Überblick zu geben, für den in der Übung heute keine Zeit war:

Also wann benutzt man was?

Wenn wir mit algebraischen Gleichungen der Form

$$ x^2 = 9 $$

arbeiten, benutzen wir $$\Leftrightarrow$$ um auszudrücken, dass bestimmte Gleichungen äquivalent sind, also unter den bekannten Umformungen semantisch gleich sind (u.a. für die Variable $$x$$). Als Beispiel:

$$\left.\begin{array}{cc}
& x^2 = 9 \\
\Leftrightarrow & \left|x \right| = 3 \end{array}\right.$$

Während also $$+$$, $$-$$, $$*$$, etc. Operatoren sind auf die wir Umformungen anwenden, benutzen wir $$\Leftrightarrow$$, aber auch die anderen logischen Operatoren, als Metaoperatoren (meta: griech. ‘über’) um über die Gleichungen Aussagen zu machen (also dass sie äquivalent sind zum Beispiel).
Ein anderer Metaoperator wäre zum Beispiel $$\Rightarrow$$ bei algebraischen Gleichungen:

$$\left.\begin{array}{cc}
& x = 3 \\
\Rightarrow& x^2 = 9 \end{array}\right.$$

In der Aussagen- und Prädikatenlogik operieren wir aber auf Aussage (bzw. Aussageformen) und dieses Mal sind die Metaoperatoren oben unsere Operatoren ($$\Leftrightarrow$$, $$\Rightarrow$$, etc.), d.h. wir brauchen andere Metaoperatoren um über die Aussagenlogik diskutieren zu können. $$\equiv$$ ist ein solcher Metaoperator, $$\not \equiv$$ auch und $$\models$$ ein anderer, den wir vielleicht später kennen lernen werden.

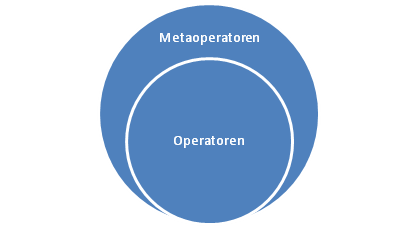
Wir benutzen $$\equiv$$ um etwas über die Gleichheit von Ausdrücken/Gleichungen der Aussagenlogik zu sagen.

$$\left.\begin{array}{ccccc}
& x^2 = 9 & & & \lnot a \Leftrightarrow \lnot b \\
\Leftrightarrow & \left|x \right| = 3 & \;\;\;\;\;\;\;\;\;\; & \equiv & a \Leftrightarrow b \end{array}\right.$$

In dieser Gegenüberstellung sieht man, wie $$\Leftrightarrow$$ rechts als normaler Operator auftritt und $$\equiv$$ als Metaoperator benutzt wird.

Tags: Äquivalenz, Metaoperatoren, Operatoren

Leave a Comment

You must be logged in to post a comment.