Die Lösung implementiert nur drawSmoothLine und benutzt double statt int in den Parametern (was mir aber nicht viel gebracht hat, weil ich dann bei kleinen Breiten Sampling-Probleme bekommen habe 😐 )

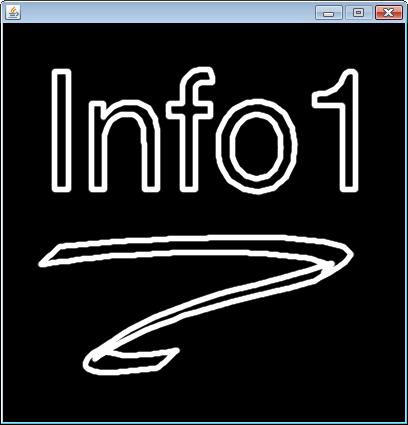


Dank an Felix Monninger für den Quellcode (den ich dann noch etwas aufpoliert und umgeschrieben um auch noch einen anderen Lösungsansatz für drawLines zu implementieren – der auch eleganter als die Musterlösung ist 🙂 )
Aufgabe3X.java
public class Aufgabe3X {
// needed for drawPoint
static int width;
static int height;
static int clamp(int min, int val, int max) {
if(val < min)
return min;
else if(val > max)
return max;
else return val;
}
// overloaded function clamp
static double clamp(double min, double val, double max) {
if(val < min)
return min;
else if(val > max)
return max;
else return val;
}
static int validX( int x ) {
return clamp( 0, x, width - 1 );
}
static int validY( int y ) {
return clamp( 0, y, height - 1 );
}
static void drawPoint(double[][] image, double color, double x, double y, double width) {
final double halfWidth = width * 0.5;
final int minX = validX( (int) Math.floor( x - halfWidth ) );
final int minY = validY( (int) Math.floor( y - halfWidth ) );
final int maxX = validX( (int) Math.ceil( x + halfWidth ) );
final int maxY = validY( (int) Math.ceil( y + halfWidth ) );
for(int i = minX ; i <= maxX ; ++i) {
for(int j = minY; j <= maxY; ++j) {
final double distanceToCenter = Math.sqrt((i-x)*(i-x)+(j-y)*(j-y));
image[i][j] += color * (1.0 - clamp(0.0, distanceToCenter / halfWidth, 1.0));
}
}
}
static void drawSmoothLine(double[][] image, double color, double x1, double y1, double x2, double y2, double width) {
final double dx = x2 - x1, dy = y2 - y1;
final double abs_dx = Math.abs( dx ), abs_dy = Math.abs( dy );
final int maxDelta = (int) Math.ceil( Math.max( abs_dx, abs_dy ) );
final double xStep = dx / maxDelta;
final double yStep = dy / maxDelta;
double x = x1;
double y = y1;
for( int i = 0 ; i < maxDelta ; i++ ) {
// hmm have to cast to int, otherwise sampling issues/Moire for small widths
drawPoint( image, color, (int) x, (int) y, width );
x += xStep;
y += yStep;
}
}
public static void main(String[] args) {
// determine optimal width and height
int[] data = Canvas.info1();
for(int i = 0; i < data.length; i += 4) {
width = Math.max( width, Math.max( Canvas.info1()[i], Canvas.info1()[i+2] ) );
height = Math.max( height, Math.max( Canvas.info1()[i+1], Canvas.info1()[i+3] ) );
}
width += 50;
height += 50;
double[][] imageMem = new double[width][height];
// zeichnet schriftzug in Dicke 7
for(int i = 0; i < Canvas.info1().length; i += 4) {
drawSmoothLine(imageMem, 1.0, Canvas.info1()[i], Canvas.info1()[i+1],
Canvas.info1()[i+2], Canvas.info1()[i+3], 7.0);
}
// zeichnet unterschiedlich dicke linien
/*drawSmoothLine(imageMem, 1.0, 90, 180, 270, 250, 30);
drawSmoothLine(imageMem, 1.0, 90, 250, 270, 180, 30);
drawSmoothLine(imageMem, 1.0, 90, 80, 270, 150, 3);
drawSmoothLine(imageMem, 1.0, 90, 150, 270, 80, 3);
drawSmoothLine(imageMem, 1.0, 90, 280, 270, 350, 40);
drawSmoothLine(imageMem, 1.0, 90, 350, 270, 280, 40);*/
Canvas.display(imageMem);
}
}
[/sourcecode]









Hi,
also, ich bin grad richtig ein wenig verzweifelt. Für mich ist klar, dass ich nie, nie, nie im Leben (zumindest zum jetzigen Zeitpunkt) diese Aufgabe so hätte lösen können. Was ich als Ausgabe hinbekommen habe, bei der 3b) ist, eine gepunktete Linie, zwar mit der richtigen Steigung, aber je nach Nachkommastellen bei der Steigung war die Linie eventuell nur durch sehr wenige Punkte “angedeutet”.
Na ja, gut, was kann man machen? Bei mir fängt es schon an, dass ich die ganzen Methoden der Math-Klasse nicht kenne .floor, .ceil und was da noch verwendet wird.
Natürlich programmieren manche schon seit sie aus dem Kindergarten kommen, aber für mich ist das (mit dem was wir in der Vorlesung machen, was ja eigtl gar nichts mit der Aufgabenstellung zu tun hat) nicht lösbar.
Es wäre vll hilfreich, wenn du, der Autor dieser Seite, mal deine Musterlsg umfassend kommentieren könntest. Das wär schon klasse. Mir erschließt sich nicht, wieso du diese “clamp”-Methode einführst, na ja, mir erschließt sich eh recht wenig dabei ;-). Also, eine Dokumentation wäre klasse, danke.
So weit mein rumgeheule, aber ich find die Aufgaben echt krass, v.a. nachdem Blatt 6 noch weit niedrigeres Niveau hatte.
LG – Mathis
Hallo Mathis,
ich kann Dir dann die Muserlösung von der Übungsleitung empfehlen, die ohne den ganzen Kram auskommt, dafür aber mehr Fallunterscheidungen durchführt.
Die Lösung, die ich hier online gestellt habe, ist eine für meine Zusatzaufgabe d) aus der Praktikumsstunde, bei der ich für die Aufgabe auch Lösungshinweise gegeben habe (statt den Punkten Kreise mit Radius width zeichnen, was drawPoint macht und die Lösung aus der b) weiterbenutzen, beim Anti-Aliasing dann additives Blending verwenden und Farbe in Abhängigkeit von der Entfernung zum Punkt-Mittelpunkt berechnen).
Die drawLine-Funktion basiert auf einer Parameterisierung der Strecke, also auf der Einführung eines zusätzlichen Parameters (normalerweise t).
In Vektorschreibweise für $$t\in \left [0,1 \right ]$$:
$$\vec{g}(t) = \begin{pmatrix}
x_1\\
y_1
\end{pmatrix}+ t \begin{pmatrix}
x_2 – x_1\\
y_2 – y_2
\end{pmatrix}$$
Die Funktion in der Lösung oben benutzt ein ganzzahliges “Intervall” im Bereich 0 bis größtes Delta (entweder entlang der x- oder y-Achse) und der zweite Vektor wird entsprechend durch die Intervallgröße dividiert. Dadurch, dass man das größtes Delta nimmt, wird auch sichergestellt, dass jeder Punkt getroffen wird.
Das ist das Wichtigste an der Funktion.
Die anderen Funktionen sind nur Hilfsfunktionen.
Ich habe diese Lösung auch nur online gestellt, weil ich sie selber interessant finde, aber es erwartet niemand, dass man sowas schreibt oder auch schon alles verstehen muss, weil das schon recht Mathe-lastig ist und schon weniger mit reinem Programmieren zu tun hat.
Grüße,
Andreas