02 Feb 09 Zusatz zu Blatt 12

Zwei kleine Zusatzaufgaben um den Nutzen der Evaluationsbäume besser zu verstehen:

Zusatzaufgaben

Wir haben im Blatt 11 in der 3. Aufgabe einen RPN-Rechner kennengelernt (und auch teilweise entwickelt). Der Rechner kann eigentlich auch nicht mehr als unserer Grammatik vom Blatt 12´ und deshalb folgende Aufgabe:

Man schreibe den Quellcode vom RPN-Rechner um, damit er auch einen Evaluationsbaum ausgibt, der mit den Funktionen vom Blatt 12 ausgewertet werden kann.
Die Musterlösung für den RPN-Rechner vom Blatt 11 gibt’s hier.

Damit soll eines deutlich gemacht werden:
Durch das Verwenden eines Evaluationsbaumes werden die Operationen auf der Struktur von der Repräsentation (RPN oder normaler Ausdruck) entkoppelt.

Folgende Zusatzaufgabe bietet sich auch noch an:

Man füge folgende Methode zu IArithmetic hinzu (und implementiere sie entsprechend)´:

List<String> GetNeededVariables();

Die Funktion soll eine Liste aller Variablennamen zurückliefern, die vom Ausdruck erwartet/benutzt werden.

Fehler im Übungsblatt

Wie ich heute erfahren habe´ gibt es einen zwar relativ leicht behebaren, aber trotzdem schweren Fehler in der Aufgabenstellung der Aufgabe 1 vom Blatt 12, der offenbar niemandem bisher aufgefallen ist´:
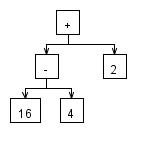
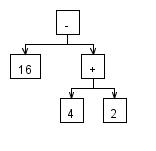
Ausdrücke wie zB. 16 – 4 – 2 oder 16 / 4 * 2 werden falsch ausgewertet!

Man kann das selbst einmal ausprobieren und es stellt sich folgende Frage: Woran liegt das?

Antwort »

Unsere Grammatik ist immer rechtsassoziativ, d.h. sie klammert immer implizit rechtseitig. Das ist bei Operatoren wie + und * kein Problem, denn diese sind assoziativ, – und / sind es aber nicht und während wir beim normalen Rechnen immer linksassoziativ arbeiten (das ist die Konvention, deswegen lassen wir solche Klammern normalerweise weg), macht unsere Grammatik genau das umgekehrte, was natürlich zu falschen Ergebnissen führt.

So sieht der korrekte Evaluationsbaum aus

Das ist der falsche Evaluationsbaum, wie er von unserem Parser erstellt wird..

Das Problem kann behoben, indem man die Grammatik wie folgt abändert:

<term> ::= <factor> { [’+’ | ’-’] <factor> }*
<factor ::= <atom> { [’*’ | ’/’] <atom> }*
<atom> ::= <const> | <var> | ’(’ <term> ’)’
<const> ::= ’0’ | [’1’-’9’ {’0’-’9’}*]
<var> ::= {’a’-’z’}+

Statt bei <term> und <factor> rekursiv zu verzweigen, erlaubt man einfach beliebig viele angehängte Additionen und Subtraktionen (Tipp: While-Schleifen im Parser-Code :-))

Quizfrage: Wieso können wir nicht die Regeln links assoziativ machen, indem wir zum Beispiel <term> ändern zu:

<term> ::= <term> { [’+’ | ’-’] <factor> }

Die Änderungen gehen in ANTLR recht schnell und im Parser-Code muss man auch nur 2 Funktionen anpassen und kurz überlegen, wie herum man die Evaluationsknoten miteinander verknüpft, aber es dürfte relativ leicht zu machen sein.

Link zu einem alten aber sehr gutem Tutorial zum Compiler- und Parser-Bau

http://www.penguin.cz/~radek/book/lets_build_a_compiler/

Grüße,
Andreas

Tags: Assoziativiät, Blatt 12, Compilerbau, Parser, Zusatzaufgaben

28 Jan 09 Blatt 12 (Lexer und Parser)

Heute befasse ich mich schon einmal früher mit dem nächsten Blatt als sonst´. Das liegt einerseits daran, dass das Thema schön ist, und andererseits daran, dass es wahrscheinlich nicht möglich ist, alles sonst so in den 3 Sunden vom Praktikum unterzubringen, dass man den größt-möglichen Nutzen daraus ziehen kann.

Vorbereitung und Informationen zu den Aufgaben

Bei dem Übungsblatt geht es um das Erstellen eines Parsers und Lexers. (Am besten einmal die Aufgabenstellung überfliegen!)

Die Aufgaben benutzen BNF-Regeln, also macht es auch Sinn, diese kurz zu wiederholen, falls man sich nicht mehr so sicher fühlt.

Wie immer verweise ich auf Wikipedia (die englischen Artikel sind hier eindeutig besser) um die Begriffe zu klären:

• Parser
• Lexical Analysis
• Recursive Descent Parser

Die einzigen Parser, die man auch ohne weitergehende Studien selber schreiben kann, sind rekursiv-absteigende Parser. Interessanterweise sind sie auch so ziemlich die einzigen Parser, deren Code leicht verständlich und wartbar ist (also insbesondere auch lesbar).

Für alle Typen gibt es sogenannte Parser Generatoren (es gibt auch Lexer Generatoren), die automatisch für einen den Quellcode eines Parsers aus vorgegebenen Regeln (BNF-Regeln meistens) erstellen.
Bekannte Beispiele sind Yacc (und Lex für den dazugehörigen Lexer Generator). Beide erstellen unlesbaren Code und um die Funktionsweise zu verstehen (bzw. um zu verstehen wie man von den Regeln auf den erstellten Code kommt) benötigt man fundiertes Wissen über Automatentheorie.

Ein für Anfänger besser geeignetes Tool (das auch Java-Code ausgibt) ist ANTLR. Zu dem Parser (der aber auch sehr mächtig ist) wurde auch ein sehr gutes Buch geschrieben (das sei hier aber nur erwähnt). Meine Beispiele benutzen später auch ANTLR.

Rekursiv-absteigende Parser

Rekursiv-absteigende Parser setzen die BNF-Regeln mehr oder weniger direkt in den Quellcode um und benutzen rekursive Aufrufe um die Regeln zu kodieren.

Wir können Exceptions benutzen um Fehler zu propagieren, doch dazu später.

Um die Struktur besser zu verstehen, möchte ich ein primitives (und nicht wirklich funktionierendes) Beispiel anführen:

Beispiel:

A ::= B | C
B ::= X Y Z*
C ::= A | C

Das würde wie folgt in (Pseudo-)Code umgesetzt werden (dabei besagt der Rückgabewert einer Funktion, ob die Regel gematcht werden konnte oder nicht (dies ist hilfreich bei Alternativen ;-)):

boolean ruleA() {
  // A ::= B | C
  return ruleB() || ruleC();
}

boolean ruleB() {
  // X
  if( !ruleX() )
    return false;

  // Y
  if( !ruleY() )
    return false;

  //  Z* (null, eines oder mehrere Zs)
  while( ruleZ() )
    ;

  return true;
}

boolean ruleC() {
  // A | C
  return ruleA() || ruleC();
}

Man kann folgendes feststellen:

• Diese Regeln bringen natürlich nichts, weil nie Zeichen (Fachwort: Literale) gematcht werden.
• Die Reihenfolge der Abarbeitung von Alternativen ist wichtig für die Programmausführung:
  Wäre C ::= C | A und würden wir das dann auch so im Quellcode schreiben (return ruleC() || ruleA()), würde, wie man unschwer erkennt, sofort eine Endlosschleife enstehen und der Regel A würde niemals Beachtung geschenkt werden.
• Die Struktur des Codes entspricht sehr stark der Struktur der Regeln – Konstrukte wie ‘mehr als eines’, etc. werden durch Schleifen kodiert, Alternativen durch “VerODERung” und Sequenzen durch “VerUNDerung”

Das ist natürlich nur ein Stück davon, wie ein Parser funktioniert (aber der wichtigste Teil, da er die Struktur beschreibt). Wir müssen jetzt “nur” noch Zeichen einlesen und “verbrauchen” können.

Lexer

In der Aufgabe (und allgemein ist es auch so) bekommen wir eine Zeichenkette und müssen aus dieser eine Struktur herausziehen.
Dazu ist es hilfreich die verschiedenen semantischen Einheiten, die man bekommt, anfangs zu klassifizieren, also zum Beispiel zu sagen: Das hier ist ein Variablenname oder das hier ist eine Zahl usw.

Dann kann man in der Grammatik bzw. im Parser direkt mit den Konzepten Zahl und Variablenname arbeiten anstatt mit irgendwelchen Zeichenregeln ala {‘a’-‘z’}+ bzw. statt mit einer Zeichenkette “x” oder “42” arbeiten zu müssen, haben wir Objekte der Typen VarToken (dessen Attribut name “x” ist) und ConstToken (dessen Attribut value 42 ist).

Der Lexer übernimmt die Aufgabe dieser Klassifierzung bzw. Zerlegung der Eingabe in ihre semantischen Einheiten:
Während ein Parser immer eine Startregel hat und von dort aus beginnt Regeln zu matchen, besteht die Aufgabe eines Lexers darin, die sogenannten Token zu bestimmen. Token sind die semantischen Einheiten, aus denen der Text besteht.

Die Aufgabe des Lexers ist also, die Zeichen einzulesen und in einem ersten Schritt zu verschiedenen Token zusammenzufassen.

Dieser Tokenstream (also Tokenstrom) wird dann vom Parser weiterverwendet (anstatt der Eingabe). In unserer Aufgabe würde der Parser nur Instanzen der Klassen VarToken, OperatorToken, etc. sehen (siehe b)) und mit diesen arbeiten.

Das heißt der Ablauf sieht folgendermaßen aus:

1. Der Lexer zerlegt die Eingabe in Tokens und speichert diese in einer Liste (welche Datenstruktur bietet sich da an?
   Antwort »

   Ein Queue ist eigentlich ideal, aber wenn wir bedenken, dass wir möglicherweise auch einmal falsch laufen und dann Tokens zurückstecken müssen, dann muss man sich etwas anderes überlegen – dazu später vielleicht mehr..

2. Der Parser bekommt den Tokenstream und fängt bei der Startregel an Token zu “verbauchen”. Die Startregel verzweigt dann an ihre Unterregeln und diese machen das gleiche´.

Keine Angst, ich gehe darauf noch genauer ein.

Beispiel

Die Aufgabenstellung unterscheidet nicht zwischen Parserregeln und Lexerregeln, sondern mischt das ganze, deswegen werde ich das jetzt auch zuerst so machen.

Im Folgenden benutze ich Grafiken und Grammatiken, die mit und für ANTLR erstellt wurden (ich werde auch den Code posten, aber keine Sorge, man muss da nicht ganz durchsteigen, sondern erst reicht die Ähnlichkeit mit den BNF-Regeln aus Info1 zu sehen).

Die ANTLR-Grammatik für unsere Aufgabe sieht wie folgt aus:

grammar arithmetic;

term 	:	factor ( ('+' | '-') term)?;
factor 	:	atom  ( ('*' | '/') factor)?;
atom	:	CONST | VAR | '(' term ')';

CONST	:	'0' | ('1'..'9' ('0'..'9')*);
VAR 	:	('a'..'z')+;

// eat whitespace
WS	:	(' '|'\n'|'\r'|'\t')+ {$channel=HIDDEN;};

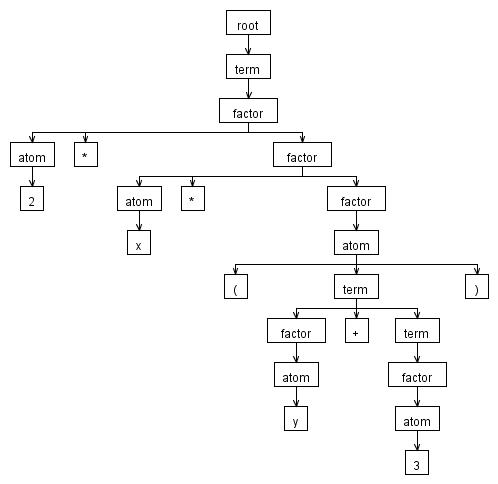
Damit können wir einen Ableitungsbaum erstellen – als Beispiel: 2 * x * (y + 3):

"2 * x * (y + 3)" als Ableitungsbaum

An den Blättern stehen jeweils die Token, die gemacht wurden. “Root” ist eine Eigenart von ANTLR und wird immer noch über die Startregel gesetzt.

Ich empfehle, dass man als Übung selber auch einmal versucht den Ableitungsbaum aufzustellen (siehe Teilaufgabe a)).

Lexer, die zweite

Die Aufgabe in der b) besteht darin, sich zu überlegen, welche Attribute die verschiedenen Token haben sollen (bzw ob überhaupt).

Die verschiedenen Klassen sollen alle IToken implementieren, damit wir später Polymorphie benutzen können und auch alle Token in einer Queue<IToken> speichern können.

Wir können dann das instanceof Schlüsselwort benutzen um später festzustellen, mit was für einem Token wir es eigentlich zu tun haben

  IToken token = tokenStream.poll();
  if( token instanceof ConstToken ) {
    // ja, token ist ein ConstToken
    ...

In der c) sollen wir dann eine Klasse Lexer schreiben, die z.B. eine statische Methode lex hat mit der Signatur:
public static Queue<IToken> lex(String expression)
Diese Methode soll, wie oben schon beschrieben, die Zeichenkette expression in eine Folge von Token aufspalten und diese zurückgeben.
Anmerkung »
Eine andere Möglichkeit wäre es eine Art von just-in-time Lexer zu schreiben, dem man mitteilt, was man erwartet und er versucht, dass dann aus der Eingabe zu parsen. Dann könnten wir aber keine statische Methode und Queue benutzen, sondern müssten ein Lexer-Objekt verwenden. Allgemein sind solche Lexer aber mächtiger, da sie eigentlich schon versteckte Parser sind 😉

Wer Interesse hat, kann mich in der Übung fragen und wir können dann mal versuchen, so einen Lexer zu implementieren – dann könnte man sich aber die b) komplett sparen ^_^

Parser, die zweite
Der Parser benutzt den Lexer um die Tokens zu bekommen und benutzt dann rekursive Funktionen (für jede Regel eine) um die Token zu verarbeiten.
Hätten wir zum Beispiel eine Regel:
<beispielRegel> ::= <const> <term> <const> {<var>}*
dann könnte der Quellcode zum Parsen der selbigen so aussehen wie gleich im Beispiel.
Dabei ist die Methode Teil der Klasse Parser und der Tokenstream vom Typ Queue<IToken> ist in einem Attribut private Queue<IToken> tokenStream gespeichert.

Desweiteren haben wir eine Exception TokensExpectedException definiert. Der Rückgabetyp ist hier im Beispiel void, könnte aber zum Beispiel vom Typ int sein, falls wir vielleicht einen Wert durch den Ausdruck berechnen möchten.
  private void parseBeispielRegel() throws TokensExpectedException {
    if( tokenStream.peek() instanceof ConstToken ) {
      tokenStream.remove();

      parseTerm();

      if( tokenStream.peek() instanceof ConstToken ) {
        tokenStream.remove();
        while( tokenStream.peek() instanceof VarToken ) {
          tokenStream.remove();
        }
      }
      else {
        // kein 2. const gefunden
        throw new TokensExpectedException( "Const expected" );
      }
    }
    else {
      // kein 1. const gefunden
      throw new TokensExpectedException( "Const expected" );
    }
  }

Alternative ohne Exceptions: »
Statt Exceptions speichern wir die Fehlermeldung in einem Attribut private String errorMessage, dafür müssen wir aber unseren Rückgabewert hergeben, um der aufrufenden Funktion mitzuteilen, ob etwas schief gegangen ist oder nicht  

  private bool parseBeispielRegel() {
    if( tokenStream.peek() instanceof ConstToken ) {
      tokenStream.remove();
      if( tokenStream.peek() instanceof ConstToken ) {
        tokenStream.remove();
        while( tokenStream.peek() instanceof VarToken ) {
          tokenStream.remove();
        }
        return true;
      }
      else {
        // kein 2. const gefunden
        errorMessage = "Const expected";
        return false;
      }
    }
    else {
      // kein 1. const gefunden
      errorMessage = "Const expected";
      return false;
    }
  }



Einleitende Aufgabe zur Aufgabe 1 und 2 für’s Praktikum:
Wir schreiben zuerst einen Interpreter, also eine Parser, der gleich die Ausdrücke interpretiert und die Werte ausrechnet und als Rückgabewert der “Regel-Funktionen” zurückgibt.
Abstrakter Syntaxbaum
Auf Wikipedia findet schon einmal eine Definition: [[wikipdia:Abstract_syntax_tree#Abstract Syntax Tree]].
Ziel der Teilaufgaben d), e) und f) ist es, anstatt die Werte direkt auszuwerten, eine Baumstruktur zu benutzen um die Struktur des geparsten Textes zu speichern. Dieser kann dann getrennt (siehe Aufgabe 2) ausgewertet werden und wir brauchen ihn nur einmal zu parsen, selbst wenn wir verschiedene Operationen auf einem Ausdruck ausführen wollen – z.B. den Wert berechnen oder feststellen, welche Variablen er braucht, etc..
Was für Knotentypen kann dieser Baum haben?
Hinweis »
Man schaue sich Bild vom Ableitungsbaum oben an und frage sich, was man alles braucht um die gesamte Struktur (also alle Informationen) zu erfassen..

Antwort »
Wir brauchen einen Knotentyp für jede Operation (+, *, -, /) und natürlich auch für die Werte und Variablen.

In der Teilaufgabe d) sollen diese Klassen mit den entsprechenden Attributen und Methoden implementiert werden. Wir implementieren wieder ein Interface – nämlich IArithmetic – um eine Baumstruktur zu ermöglichen.
Dazu möchte ich auf Composite Pattern verweisen´, damit man versteht, welche Idee dahinter steckt.
Tree Walker
Bei der Aufgabe 2 geht es darum, einen mit dem Parser erstellten Evaluationsbaum zudurchlaufen und die Ausdrücke auszuwerten um den Wert des gesamtem Ausdruckes zu bestimmen. Dazu fügen wir eine Methode public int evaluate() zum Interface IArithmetic hinzu und implementieren sie dann für jeden Knotentyp derart, dass der Knotentyp seine Teilausdrücke auswertet und seine Operation darauf anwendet (falls er Teilausdrücke hat und ein Operator ist :D).
Dank Polymorphie und dem Composite Pattern geht das relativ schmerzlos.
Zusatzaufgabe (oder alternative Aufgabe)
Statt das Interface nachträglich zu ändern, kann man ein anderes, ebenfalls sehr mächtiges Design Pattern benutzen: das Visitor Pattern´ .
Damit können wir beliebig Operationen auf dem ganzen Baum definieren (wie das Auswerten oder Variablen bestimmen, etc.) ohne mehr als einmal das Interface und die Knotentypen anpassen zu müssen.
Das ist aber wirklich nur eine Zusatzaufgabe, falls noch Zeit bleibt.
Falls ich aber noch Zeit finde, werde ich auch noch Lösungen für alle Aufgaben in ANTLR entwickeln – es dürften nicht mehr als 100 Zeilen sein, aber mein ANTLR-Wissen ist etwas eingerostet..
Grüße,

Andreas
						
Tags: ANTLR, Blatt 12, Composite Pattern, Exceptions, Lexer, Parser, Vistor Pattern
			            

			
Filed in Aufgaben, Off-Topic, Tutorübung, Zur Vorlesung with 0 Comments 

					
21 Dec 08 Kleine Zusatzaufgabe zur Landau-Notation
     

			
Ich weiß nicht, wer schon alles mit der Landau-Notation vertraut ist (und auch mit der Komplexitätstheorie von Algorithmen). Aber als kleine Zusatzaufgabe´ zur Hausaufgabe vom Blatt 6 (weil ich sie gerade korrigiere) folgendes:
Welche Laufzeiten (ala O(n), etc.) hat der Primzahltest normalerweise, wenn wir ihn so programmieren wie in der Musterlösung zur 1a)?
static boolean isPrime(int p ) {
  for( int k = 2 ; k * k <= p ; k++ ) {
    if( p % k == 0 ) {
      return false;
    }
  }
  return true;
}
[/sourcecode]
Fleißaufgabe:

Wie sieht's mit den Laufzeiten der anderen Funktionen aus?
Man kann die Lösung wahrscheinlich leicht mit Google finden, aber es an sich ganz nett da selber einmal darauf zukommen.
Hinweis »
Die Aufgabenstellung ist bewusst so schwammig gewählt, damit man sich erst einmal Gedanken darüber machen muss, was genau eigentlich gemessen/beschrieben werden soll ´.

Das Ergebnis ist nicht   $$ \mathbf{ O(n) }$$ und auch nicht   $$ \mathbf{O(\sqrt{x})}$$.


									            

			
Filed in Aufgaben with 5 Comments 

					
19 Dec 08 Blatt 8, Zusatzaufgaben
     

			
Zum Blatt 8 folgende Zusatzaufgaben:
Aufgabe 2:
j) Schreiben Sie in der Klasse TimeTable eine Methode
public int addTrainArrival( string nameOfTrain, Date arrivalTime ) { … }
welche zur gegebenen Zeit versucht ein freies Gleis für den Zug zu finden und falls dies möglich ist eine TrainConnection mit den Informationen erstellt und hinzugefügt. Die Methode gibt dies Nummer des Gleises zurück, falls ein Gleis gefunden wurde, ansonsten -1.
k) Schreiben Sie in der Klasse TimeTable eine Methode optimizeForTransitPassengers, die die TrainConnections in der TimeTable dahingehend optimiert, dass Passagiere von Zügen, die zu ähnlichen Zeiten ankommen, möglichst wenige Gleise von einem Zug zum nächsten laufen müssen, falls sie umsteigen wollen´.
Hinweis:
Es ist sinnvoll den Fahrplan um mehr TrainConnections zu erweitern – am besten mit einer For-Schleife weitere Einträge hinzufügen.
Aufgabe 3:
d) Natürlich die Potenzmenge bestimmen 

Also:
public staic <S> Set<Set<S>> powerSet( Set<S> s ) {…}
									            

			
Filed in Aufgaben, Tutorübung with 0 Comments 

					
12 Dec 08 Blatt 7 Aufgabe 3
     

			
Ein kleines “Gerüst” für die Aufgabe 3: aufgabe3.zip
Zusatzaufgabe:
d) Füge zuerst zu Lines eine Funktion hinzu
static void drawLine( double[][] image, double color,
                            double x1, double y1, double x2,
                            double y2, double width )
die eine Linie mit variabler Breite width zeichnet (linkes Teilbild unten) und dann eine Funktion
static void drawSmoothLine( double[][] image, double color,
                            double x1, double y1, double x2,
                            double y2, double width )
die analog zu drawLine eine weiche Line der Breite width einzeichnet. So wie die Linie auf dem rechten Teilbild:

Lösung »

Die Lösung implementiert nur drawSmoothLine und benutzt double statt int in den Parametern (was mir aber nicht viel gebracht hat, weil ich dann bei kleinen Breiten Sampling-Probleme bekommen habe 😐 )


Dank an Felix Monninger für den Quellcode (den ich dann noch etwas aufpoliert und umgeschrieben um auch noch einen anderen Lösungsansatz für drawLines zu implementieren – der auch eleganter als die Musterlösung ist  )
Aufgabe3X.java
public class Aufgabe3X {
  // needed for drawPoint
  static int width;
  static int height;

  static int clamp(int min, int val, int max) {
    if(val < min)
      return min;
    else if(val > max)
      return max;
    else return val;
  }

  // overloaded function clamp
  static double clamp(double min, double val, double max) {
    if(val < min)
      return min;
    else if(val > max)
      return max;
    else return val;
  }

  static int validX( int x ) {
    return clamp( 0, x, width - 1 );
  }

  static int validY( int y ) {
    return clamp( 0, y, height - 1 );
  }

  static void drawPoint(double[][] image, double color, double x, double y, double width) {
    final double halfWidth = width * 0.5;

    final int minX = validX( (int) Math.floor( x - halfWidth ) );
    final int minY = validY( (int) Math.floor( y - halfWidth ) );

    final int maxX = validX( (int) Math.ceil( x + halfWidth ) );
    final int maxY = validY( (int) Math.ceil( y + halfWidth ) );

    for(int i = minX ; i <= maxX ; ++i) {
      for(int j = minY; j <= maxY; ++j) {
        final double distanceToCenter = Math.sqrt((i-x)*(i-x)+(j-y)*(j-y));
        image[i][j] += color * (1.0 - clamp(0.0, distanceToCenter / halfWidth, 1.0));
      }
    }
  }

  static void drawSmoothLine(double[][] image, double color, double x1, double y1, double x2, double y2, double width) {
    final double dx = x2 - x1, dy = y2 - y1;
    final double abs_dx = Math.abs( dx ), abs_dy = Math.abs( dy );

    final int maxDelta = (int) Math.ceil( Math.max( abs_dx, abs_dy ) );

    final double xStep = dx / maxDelta;
    final double yStep = dy / maxDelta;

    double x = x1;
    double y = y1;
    for( int i = 0 ; i < maxDelta ; i++ ) {
      // hmm have to cast to int, otherwise sampling issues/Moire for small widths
      drawPoint( image, color, (int) x, (int) y, width );
      x += xStep;
      y += yStep;
    }
  }

  public static void main(String[] args) {
    // determine optimal width and height
    int[] data = Canvas.info1();
    for(int i = 0; i < data.length; i += 4) {
      width = Math.max( width, Math.max( Canvas.info1()[i], Canvas.info1()[i+2] ) );
      height = Math.max( height, Math.max( Canvas.info1()[i+1], Canvas.info1()[i+3] ) );
    }
    width += 50;
    height += 50;

    double[][] imageMem = new double[width][height];

    // zeichnet schriftzug in Dicke 7
    for(int i = 0; i < Canvas.info1().length; i += 4) {
      drawSmoothLine(imageMem, 1.0, Canvas.info1()[i], Canvas.info1()[i+1],
                             Canvas.info1()[i+2], Canvas.info1()[i+3], 7.0);
    }

    // zeichnet unterschiedlich dicke linien

    /*drawSmoothLine(imageMem, 1.0, 90, 180, 270, 250, 30);
    drawSmoothLine(imageMem, 1.0, 90, 250, 270, 180, 30);

    drawSmoothLine(imageMem, 1.0, 90, 80, 270, 150, 3);
    drawSmoothLine(imageMem, 1.0, 90, 150, 270, 80, 3);

    drawSmoothLine(imageMem, 1.0, 90, 280, 270, 350, 40);
    drawSmoothLine(imageMem, 1.0, 90, 350, 270, 280, 40);*/

    Canvas.display(imageMem);
  }
}
[/sourcecode]


						
Tags: Anti-Aliasing, Aufgabe 3, Blatt 7
			            

			
Filed in Aufgaben, Tutorübung with 2 Comments 

					
10 Dec 08 Aufgaben zur prozeduralen Programmierung (TODO)
     

			
Hier ein paar Übungsaufgabe zur prozeduralen Programmierung. Vorab kann ich aber nur empfehlen die Aufgaben aus dem Praktikum auch zu wiederholen und zwar so lange, bis man die Schleifen-Konstrukte im Schlaf beherrscht und die Aufgaben auch so kein Problem mehr darstellen.
Außerdem empfiehlt es sich generell zusätzlich zu Vorlesungen noch weitere Literatur zu benutzen, in unserem Falle also einerseits ein Buch zum theoretischen Teil der Vorlesung (es empfiehlt sich wahrscheinlich das Buch von Prof. Broy) und eines für Java, wobei da wohl jedes Java-Buch gleichermaßen geeignet ist.

Die andere Darstellung der Inhalte ist oft hilfreich und man bekommt ein besseres Gefühl für die Sprache selber – wobei natürlich das Schreiben von Java-Code die beste Möglichkeit ist um die Sprache zu lernen!
Code Convention für Java
Diese Aufgabe wird wahrscheinlich noch in einen eigenen Blogeintag erweitert werden, aber insbesondere in Hinblick auf die Klausur (für die Korrektur) und die Tatsache, dass wir jetzt langsam richtig in die Programmierung einsteigen, möchte ich eine Link posten, der für Anfänger hilfreich sein sollte und auch für diejenigen, die schon mehr Java programmiert haben, interessant sein kann:
Code Conventions for the Java Programming Language
Hierbei handelt es sich um ein ziemlich ausführliches Handbuch, wie der Java-Code von Sun (den Erfindern von Java) formatiert werden soll.

Man kann sich über die genaue Formatierung von Code streiten (in einschlägigen Foren finden sich mehr als genügend Beispiele dafür), aber auf jeden Fall sollte der Quellcode, den man schreibt einheitlich formatiert werden und auf eine Art und Weise, die sowohl übersichtlich ist als auch der Syntax der Sprache gerecht wird.
Beim jetzigen Stand in den Übungen kann ich das Kapitel 1 Introduction (ein sehr kurzer Text) und das Kapitel 7 Statements empfehlen.

Ich bin selber nicht mit allem einverstanden, was teilweise in den anderen Kapiteln steht, aber dieses Dokument ist ein guter Einstiegspunkt und gibt gute Hinweise darauf, wie man seinen Code formatieren sollte.
Als generelle $$\pi$$ mal Daumen-Regel kann ich ansonsten nur sagen: “Jede Anweisung in ihrer eigenen Zeile.”
Aufgaben
Texthaus
Als Vorbeitung empfiehlt sich die Aufgabe 2 vom Übungsblatt 6.
Ziel der Aufgabe ist es eine Prozedur zu schreiben, die ein Haus als Text ausgibt:
    x
   x x
  x   x
 x     x
x       x
xxxxxxxxx
x       x
x       x
x       x
x       x
xxxxxxxxx

Schreibe eine Prozedur, die in Abhängigkeit von einem positiven Integer-Parameter n > 1 (Wieso?) ein Haus (in der obigen Form) der Breite n mit System.print() und System.println() zeichnet und auf der Konsole ausgibt.

Hinweise:

Für ungerade n ist das Haus oben ein Beispiel – wie sieht das Haus für gerade n aus? (Lösungsskizze!)

Zusätzlich
Damit das Haus besser isoliert ist, soll das Innere des Dachs mit ^ und die Hauswand mit # ausgefüllt werden.

Außerdem sind Hochhäuser in, deswegen wäre es schön, wenn das Haus mehrere Stockwerke haben könnte – man füge also eine Parameter m > 0 hinzu, der angibt, wie viele Stockwerke das Haus haben soll und zeichne das Haus entsprechend.

Permutationen
Permutationen sind sehr leicht mit Schleifen zu erzeugen, deswegen:
Man schreibe eine Funktion <T> Seq<Seq<T>> getPermutations( Seq<T> set ), die alle Permutationen von set zurückgibt.
Hinweise:

Es lohnt sich auf jeden Fall die übliche Vorgehensweise zu probieren, selbst wenn die Aufgabe abschreckend wirkt:
Ein paar einfache Beispiele per Hand lösen, dann schauen, wie man die Lösungen in Teilprobleme zerlegen kann (also wie man eine Permutation mit Hilfe von Teilpermutationen bestimmen kann).

Hierbei können (wie so oft sonst auch) kleine Skizzen nützlich sein.
Achtung:
PS: Dieser Eintrag ist TODO, d.h. ich werde hier wahrscheinlich noch ein paar Dinge anfügen, nur wollte ich, weil ich momentan einiges um die Ohren habe und die Klausur ansteht, auch zumindest diese beiden kleinen Aufgaben nicht vorenthalten.
Feedback ist, wie immer, erwünscht.
									            

			
Filed in Aufgaben with 1 Comment 

					
28 Nov 08 Aufgaben zu Rekursiven Funktionen
     

			
Hier noch einiges Übungsaufgaben, die jeder für sich lösen kannHinweis.
Operationen auf Sequenzen $$\mathrm{Seq} \langle T \rangle$$

Wiederhole generische Funktionen und Sequenzen auf dem Merkblatt zu FJava.
Schreibe die Funktionen <T> int length( Seq<T> seq ), <T> T last( Seq<T> seq ) ohne irgendwo nachzuschlagen.
Entwickle eine Funktion <T> Seq<T> reverse( Seq<T> seq ), die eine Sequenz umdreht – aus [1,2,3,4] würde [4,3,2,1] werden.
Entwickle eine Funktion <T> T _getNth( Seq<T> seq, int n ), die das n-te Element ($$n \ge 0$$) aus der Sequenz zurückgibt. Wir fangen an bei 0 zu zählen, also _getNth( [0,1,2,3,4], 3 ) = 3.
Entwickle eine Funktion <T> T getNth( Seq<T> seq, int n ), die das n-te Element aus der Sequenz zurückgibt. Ist $$n < 0$$, so gebe das $$-n$$-te Element vom Ende der Sequenz zurück, also getNth( [4,3,2,1], -2 ) = 2.
Schreibe eine Funktion <T> boolean isEqual( Seq<T> a, Seq<T> b ), die überprüft, ob alle Elemente in der Sequenz a gleich denen in b sind (in der gleichen Reihenfolge), also isEqual( [1,2,3], [1,2,3] ) = true, aber isEqual( [1,2,3], [3,2,1] ) = false und natürlich isEqual( [], [] ) = true und isEqual( [1,2], [1,2,3] ) = false.

Beachte hierbei, dass T auch String sein kann, also muss man vergleichen mit a.equals( b ) für a, b aus der Sorte T´.
Schreibe eine Funktion <T> boolean isPalindrome( Seq<T> a ), die überprüft, ob a ein Palindrom ist, d.h. a ist vorwärts und rückwärts gelesen gleich.
Schreibe eine Funktion <T> boolean inSeq( T element, Seq<T> seq ), die überprüft, ob element in der Sequenz seq vorkommt.

Beachte hierbei, dass T auch String sein kann, also muss man vergleichen mit a.equals( b ) für a, b aus der Sorte T.


Entwickle eine Funktion <T> int count( Seq<T> seq, T element ), die zurückgibt, wie oft element in der Sequenz seq vorkommt.

Beachte hierbei, dass T auch String sein kann, also muss man vergleichen mit a.equals( b ) für a, b aus der Sorte T.
Entwickle eine Funktion <T> int remove( Seq<T> seq, T element ), die alle Vorkommen von element aus seq löscht.

Sequenzen als Mengen
Mengen sind ein Spezialfall von Sequenzen, bei denen jedes Element höchstens einmal vorkommen darf und die Reihenfolge der Elemente egal ist (wenn man auf Gleichheit o.ä. prüfen will).

Schreibe eine Funktion <T> boolean isSet( Seq<T> seq ), die zurückgibt, ob seq eine Menge ist, also ob jedes Element höchstens einmal in seq vorkommt.
Schreibe eine Funktion <T> boolean inSet( T element, Seq<T> set ), die zurückgibt, ob element in set ist.´
Schreibe eine Funktion <T> Seq<T> insertIntoSet( Seq<T> set, T element ), die element zur Menge set hinzufügt. Wenn für set gilt: isSet( set ) = true, dann soll dies auf für den Rückgabewert von insertIntoSet gelten.
Schreibe analog eine Funktion removeFromSet.
Entwickle Funktionen union und intersect die analog Mengen vereinen und schneiden.
Entwickle eine Funktion <T> boolean isSubset( Seq<T> subSet, Seq<T> set ), die überprüft, ob $$ \mathbf{subSet} \subseteq  \mathbf{set} $$ gilt.
Entwickle eine Funktion <T> boolean isSetEqual( Seq<T> aSet, Seq<T> bSet ), die überprüft, ob die Mengen aSet und bSet gleich sind.

Wieso ist isSetEqual für Mengen weniger effizient als isEqual für Sequenzen?´
Entwickle eine Funktion <T> Seq<Seq<T>> powerSet( Seq<T> set ), welche die Potenzmenge der Menge set konstruiert. Für jedes Sequenz s aus dem Rückgabewert gilt also: isSet( s ) = true und isSubset( s, set ) = true.

Hinweis: Man entwickle zuerst eine Funktion <T> Seq<Seq<T>> setsWithoutOneElement( Seq<T> set ), welche alle Teilmengen von set zurückgibt, die ein Element weniger enthalten.´

Operationen auf Sequenzen von Sequenzen´

Entwickle eine Funktion <T> Seq<Seq<T>> expandFront( Seq<T> seq, Seq<T> choices ), die alle Sequenzen s zurückgibt, für die gilt: isEqual( rest( s ), seq ) = true und inSeq( first( s ), choices ) = true.´
Entwickle eine analoge Funktion <T> Seq<Seq<T>> expandBack( Seq<T> seq, Seq<T> choices ), für die obigen Bedingungen für reverse( s ) statt s gelten. Wie sehen dann Nachbedingungen für expandBack aus?´
Schreibe die Funktion <T> Seq<Seq<T>> expandAcyclicFront( Seq<T> seq, Seq<T> choices ), die nur Sequenzen s zurückgibt für die gilt: inSeq( first( s ), rest( s ) ) = false.
Schreibe analog zu expandBack, die Funktion expandAcyclicBack.
Entwickle eine Funktion <T> Seq<T> getNeighbors( Seq<Seq<T>> neighborSeq, T node ), die den Rest der Untersequenz zurückgibt, die als erstes Element node hat, oder die leere Sequenz, falls es keine solche Sequenz gibt, wobei jede Sequenz von neighborSeq ein anderes erstes Element besitzt, also wäre [[1,2],[1,2,3] keine gültige Sequenz.

Beispiel: getNeighbors( [[1,2,3], [2,1,4], [3,1]], 2 ) = [1, 4].

Reflexive, Transitive Hüllen
Die reflexive, transitive Hülle $$ \rightarrow ^{\star} $$ über einer Menge $$\mathbf{G}$$ und einer Relation $$ \rightarrow : \mathbf{G} \times \mathbf{G} \rightarrow \mathbf{G}, \left( a, b \right) \mapsto a \rightarrow b $$ (gelesen: “a zeigt zu b”) ist folgendermaßen definiert´:
$$ \\\\

\forall a, b \in \mathbf{G}:\\

\begin{array}{lcl}

a \rightarrow ^ 0 b & :\Leftrightarrow & \begin{cases}

true & \text{ : } a = b  \\

false & \text{ : } a \not = b
\end{cases} \\\\

a \rightarrow ^ 1 b & : \Leftrightarrow & a \rightarrow b \\\\

a \rightarrow ^{n+1} b & : \Leftrightarrow & \exists x \in \mathbf{G}: a \rightarrow ^{n} x \land x \rightarrow b\\

\\

\\

a \rightarrow ^ {\star} b & : \Leftrightarrow & \exists n \in \mathbb{N}: a \rightarrow ^ n b

\end{array}

$$
Wir können diese Konstruktion auch in FJava nachvollziehen, wenn wir die Relation in einer Adjanzentliste speichern, d.h. gilt:
$$

\mathbf{ G = \left \{ a, b, c, d, e \right \} }

$$

und

$$

\mathbf{

a \rightarrow b, a \rightarrow c, a \rightarrow d, b \rightarrow c, b \rightarrow d,

c \rightarrow a, d \rightarrow b, d \rightarrow  e }

$$

so speichern wir das als:

$$\mathbf{seq := \left[\left[a, b, c, d \right], \left[b, c, d \right], \left[c, a \right], \left[d, b, e \right], \left[ e \right] \right]}$$

Sprich: Jedes Element kommt genau einmal als erstes Element in einer Untersequenz vor und der Rest der jeweiligen Untersequenz gibt die Elemente an, auf die das erste Element “zeigt”.

Dann können wir aus $$\mathbf{seq}$$ sowohl $$\mathbf{G}$$, als auch $$\rightarrow$$ bestimmen, da diese durch die Adjazenzliste eindeutig festgelegt sind.
Außerdem können wir getNeighbors benutzen um aus solch einer Sequenz, alle Elemente zu finden, auf die ein bestimmes zeigt.

Im Folgenden sei mit neighborSeq immer die Adjazenzliste von $$ \rightarrow $$ bezeichnet.
In dem Beispiel von oben: getNeighbors( seq, “a” ) = [ “b”, “c”, “d” ].

Schreibe eine Funktion <T> Seq<Seq<T>> zeroHull( Seq<Seq<T>> neighborSeq ), die für die Relation, die durch die Adjazenzliste neighborSeq bestimmt ist, die Adjazenzliste aller Elemente bestimmt für $$ \rightarrow^0 $$.

Im Beispiel von oben wäre dies:

$$\mathbf{seq := \left[\left[a, a \right], \left[b, b \right], \left[c, c \right], \left[d, d\right], \left[ e, e \right] \right]}$$
Entwickle eine Funktion <T> Seq<T> squareHullForElement( Seq<Seq<T>> neighborSeq, T element ), die die Menge aller Elemente x enthält, die von element in zwei Schritten erreichbar sind, also: $$ \mathbf{ \exists y \in G: element \rightarrow y \rightarrow x }$$
Entwickle eine Funktion <T> Seq<Seq<T>> squareHull( Seq<Seq<T>> neighborSeq ), die $$ \rightarrow ^2 $$ von neighborSeq zurückgibt.
Entwickle eine Funktion <T> Seq<T> nthHull( Seq<Seq<T>> neighborSeq, int n ), die für $$ n \ge 0 $$ die n-te Hülle von $$\rightarrow$$ bestimmt, also $$ \rightarrow^n $$.

Hinweis:

Man schreibe zuerst eine Funktion <T> Seq<Seq<T>> concatenateRelation( Seq<Seq<T> neighborSeqN, Seq<Seq<T>> neighborSeq ), die zwei Relationen $$ \prec $$  und $$ \propto $$, die durch neighborSeqN bzw. neighborSeq beschrieben werden, auf $$ \mathbf{G}$$ hintereinanderausführt und die sich ergebende Relation $$ \sqsubset $$ als Adjanzenzliste zurückgibt, so dass für alle Teilsequenzen mit erstem Element e und restlichen Elementen x, gilt:

$$ \mathbf{ \exists y \in G: e \prec y \land y \propto x :\Leftrightarrow e \sqsubset x }$$.´
Schreibe eine Funktion <T> Seq<Seq<T>> transitiveHull( Seq<Seq<T>> neighborSeq ), die $$ \rightarrow ^{\star} $$ konstruiert. Die Funktion kann immer terminieren, da $$ \mathbf{G} $$ endlich ist.

						
Tags: Add new tag, Aufgaben, FJava, Mengen, Sequenzen, Transitive Hülle
			            

			
Filed in Aufgaben with 0 Comments