28 Jan 09 Blatt 12 (Lexer und Parser)

Heute befasse ich mich schon einmal früher mit dem nächsten Blatt als sonst´. Das liegt einerseits daran, dass das Thema schön ist, und andererseits daran, dass es wahrscheinlich nicht möglich ist, alles sonst so in den 3 Sunden vom Praktikum unterzubringen, dass man den größt-möglichen Nutzen daraus ziehen kann.

Vorbereitung und Informationen zu den Aufgaben

Bei dem Übungsblatt geht es um das Erstellen eines Parsers und Lexers. (Am besten einmal die Aufgabenstellung überfliegen!)

Die Aufgaben benutzen BNF-Regeln, also macht es auch Sinn, diese kurz zu wiederholen, falls man sich nicht mehr so sicher fühlt.

Wie immer verweise ich auf Wikipedia (die englischen Artikel sind hier eindeutig besser) um die Begriffe zu klären:

Die einzigen Parser, die man auch ohne weitergehende Studien selber schreiben kann, sind rekursiv-absteigende Parser. Interessanterweise sind sie auch so ziemlich die einzigen Parser, deren Code leicht verständlich und wartbar ist (also insbesondere auch lesbar).

Für alle Typen gibt es sogenannte Parser Generatoren (es gibt auch Lexer Generatoren), die automatisch für einen den Quellcode eines Parsers aus vorgegebenen Regeln (BNF-Regeln meistens) erstellen.
Bekannte Beispiele sind Yacc (und Lex für den dazugehörigen Lexer Generator). Beide erstellen unlesbaren Code und um die Funktionsweise zu verstehen (bzw. um zu verstehen wie man von den Regeln auf den erstellten Code kommt) benötigt man fundiertes Wissen über Automatentheorie.

Ein für Anfänger besser geeignetes Tool (das auch Java-Code ausgibt) ist ANTLR. Zu dem Parser (der aber auch sehr mächtig ist) wurde auch ein sehr gutes Buch geschrieben (das sei hier aber nur erwähnt). Meine Beispiele benutzen später auch ANTLR.

Rekursiv-absteigende Parser

Rekursiv-absteigende Parser setzen die BNF-Regeln mehr oder weniger direkt in den Quellcode um und benutzen rekursive Aufrufe um die Regeln zu kodieren.

Wir können Exceptions benutzen um Fehler zu propagieren, doch dazu später.

Um die Struktur besser zu verstehen, möchte ich ein primitives (und nicht wirklich funktionierendes) Beispiel anführen:

Beispiel:

A ::= B | C
B ::= X Y Z*
C ::= A | C

Das würde wie folgt in (Pseudo-)Code umgesetzt werden (dabei besagt der Rückgabewert einer Funktion, ob die Regel gematcht werden konnte oder nicht (dies ist hilfreich bei Alternativen ;-)):

boolean ruleA() {
  // A ::= B | C
  return ruleB() || ruleC();
}

boolean ruleB() {
  // X
  if( !ruleX() )
    return false;

  // Y
  if( !ruleY() )
    return false;

  //  Z* (null, eines oder mehrere Zs)
  while( ruleZ() )
    ;

  return true;
}

boolean ruleC() {
  // A | C
  return ruleA() || ruleC();
}

Man kann folgendes feststellen:

Diese Regeln bringen natürlich nichts, weil nie Zeichen (Fachwort: Literale) gematcht werden.
Die Reihenfolge der Abarbeitung von Alternativen ist wichtig für die Programmausführung:
Wäre C ::= C | A und würden wir das dann auch so im Quellcode schreiben (return ruleC() || ruleA()), würde, wie man unschwer erkennt, sofort eine Endlosschleife enstehen und der Regel A würde niemals Beachtung geschenkt werden.
Die Struktur des Codes entspricht sehr stark der Struktur der Regeln – Konstrukte wie ‘mehr als eines’, etc. werden durch Schleifen kodiert, Alternativen durch “VerODERung” und Sequenzen durch “VerUNDerung”

Das ist natürlich nur ein Stück davon, wie ein Parser funktioniert (aber der wichtigste Teil, da er die Struktur beschreibt). Wir müssen jetzt “nur” noch Zeichen einlesen und “verbrauchen” können.

Lexer

In der Aufgabe (und allgemein ist es auch so) bekommen wir eine Zeichenkette und müssen aus dieser eine Struktur herausziehen.
Dazu ist es hilfreich die verschiedenen semantischen Einheiten, die man bekommt, anfangs zu klassifizieren, also zum Beispiel zu sagen: Das hier ist ein Variablenname oder das hier ist eine Zahl usw.

Dann kann man in der Grammatik bzw. im Parser direkt mit den Konzepten Zahl und Variablenname arbeiten anstatt mit irgendwelchen Zeichenregeln ala {‘a’-‘z’}+ bzw. statt mit einer Zeichenkette “x” oder “42” arbeiten zu müssen, haben wir Objekte der Typen VarToken (dessen Attribut name “x” ist) und ConstToken (dessen Attribut value 42 ist).

Der Lexer übernimmt die Aufgabe dieser Klassifierzung bzw. Zerlegung der Eingabe in ihre semantischen Einheiten:
Während ein Parser immer eine Startregel hat und von dort aus beginnt Regeln zu matchen, besteht die Aufgabe eines Lexers darin, die sogenannten Token zu bestimmen. Token sind die semantischen Einheiten, aus denen der Text besteht.

Die Aufgabe des Lexers ist also, die Zeichen einzulesen und in einem ersten Schritt zu verschiedenen Token zusammenzufassen.

Dieser Tokenstream (also Tokenstrom) wird dann vom Parser weiterverwendet (anstatt der Eingabe). In unserer Aufgabe würde der Parser nur Instanzen der Klassen VarToken, OperatorToken, etc. sehen (siehe b)) und mit diesen arbeiten.

Das heißt der Ablauf sieht folgendermaßen aus:

Der Lexer zerlegt die Eingabe in Tokens und speichert diese in einer Liste (welche Datenstruktur bietet sich da an?
Antwort »
Ein Queue ist eigentlich ideal, aber wenn wir bedenken, dass wir möglicherweise auch einmal falsch laufen und dann Tokens zurückstecken müssen, dann muss man sich etwas anderes überlegen – dazu später vielleicht mehr..
Der Parser bekommt den Tokenstream und fängt bei der Startregel an Token zu “verbauchen”. Die Startregel verzweigt dann an ihre Unterregeln und diese machen das gleiche´.

Keine Angst, ich gehe darauf noch genauer ein.

Beispiel

Die Aufgabenstellung unterscheidet nicht zwischen Parserregeln und Lexerregeln, sondern mischt das ganze, deswegen werde ich das jetzt auch zuerst so machen.

Im Folgenden benutze ich Grafiken und Grammatiken, die mit und für ANTLR erstellt wurden (ich werde auch den Code posten, aber keine Sorge, man muss da nicht ganz durchsteigen, sondern erst reicht die Ähnlichkeit mit den BNF-Regeln aus Info1 zu sehen).

Die ANTLR-Grammatik für unsere Aufgabe sieht wie folgt aus:

grammar arithmetic;

term 	:	factor ( ('+' | '-') term)?;
factor 	:	atom  ( ('*' | '/') factor)?;
atom	:	CONST | VAR | '(' term ')';

CONST	:	'0' | ('1'..'9' ('0'..'9')*);
VAR 	:	('a'..'z')+;

// eat whitespace
WS	:	(' '|'\n'|'\r'|'\t')+ {$channel=HIDDEN;};

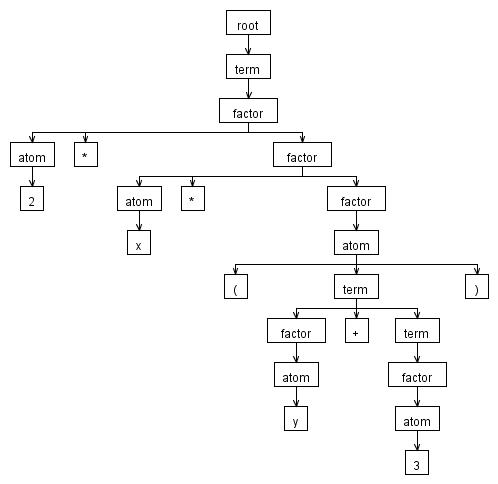
Damit können wir einen Ableitungsbaum erstellen – als Beispiel: 2 * x * (y + 3):

"2 * x * (y + 3)" als Ableitungsbaum

An den Blättern stehen jeweils die Token, die gemacht wurden. “Root” ist eine Eigenart von ANTLR und wird immer noch über die Startregel gesetzt.

Ich empfehle, dass man als Übung selber auch einmal versucht den Ableitungsbaum aufzustellen (siehe Teilaufgabe a)).

Lexer, die zweite

Die Aufgabe in der b) besteht darin, sich zu überlegen, welche Attribute die verschiedenen Token haben sollen (bzw ob überhaupt).

Die verschiedenen Klassen sollen alle IToken implementieren, damit wir später Polymorphie benutzen können und auch alle Token in einer Queue<IToken> speichern können.

Wir können dann das instanceof Schlüsselwort benutzen um später festzustellen, mit was für einem Token wir es eigentlich zu tun haben

  IToken token = tokenStream.poll();
  if( token instanceof ConstToken ) {
    // ja, token ist ein ConstToken
    ...

In der c) sollen wir dann eine Klasse Lexer schreiben, die z.B. eine statische Methode lex hat mit der Signatur:
public static Queue<IToken> lex(String expression)
Diese Methode soll, wie oben schon beschrieben, die Zeichenkette expression in eine Folge von Token aufspalten und diese zurückgeben.
Anmerkung »
Eine andere Möglichkeit wäre es eine Art von just-in-time Lexer zu schreiben, dem man mitteilt, was man erwartet und er versucht, dass dann aus der Eingabe zu parsen. Dann könnten wir aber keine statische Methode und Queue benutzen, sondern müssten ein Lexer-Objekt verwenden. Allgemein sind solche Lexer aber mächtiger, da sie eigentlich schon versteckte Parser sind 😉

Wer Interesse hat, kann mich in der Übung fragen und wir können dann mal versuchen, so einen Lexer zu implementieren – dann könnte man sich aber die b) komplett sparen ^_^

Parser, die zweite
Der Parser benutzt den Lexer um die Tokens zu bekommen und benutzt dann rekursive Funktionen (für jede Regel eine) um die Token zu verarbeiten.
Hätten wir zum Beispiel eine Regel:
<beispielRegel> ::= <const> <term> <const> {<var>}*
dann könnte der Quellcode zum Parsen der selbigen so aussehen wie gleich im Beispiel.
Dabei ist die Methode Teil der Klasse Parser und der Tokenstream vom Typ Queue<IToken> ist in einem Attribut private Queue<IToken> tokenStream gespeichert.

Desweiteren haben wir eine Exception TokensExpectedException definiert. Der Rückgabetyp ist hier im Beispiel void, könnte aber zum Beispiel vom Typ int sein, falls wir vielleicht einen Wert durch den Ausdruck berechnen möchten.
  private void parseBeispielRegel() throws TokensExpectedException {
    if( tokenStream.peek() instanceof ConstToken ) {
      tokenStream.remove();

      parseTerm();

      if( tokenStream.peek() instanceof ConstToken ) {
        tokenStream.remove();
        while( tokenStream.peek() instanceof VarToken ) {
          tokenStream.remove();
        }
      }
      else {
        // kein 2. const gefunden
        throw new TokensExpectedException( "Const expected" );
      }
    }
    else {
      // kein 1. const gefunden
      throw new TokensExpectedException( "Const expected" );
    }
  }

Alternative ohne Exceptions: »
Statt Exceptions speichern wir die Fehlermeldung in einem Attribut private String errorMessage, dafür müssen wir aber unseren Rückgabewert hergeben, um der aufrufenden Funktion mitzuteilen, ob etwas schief gegangen ist oder nicht  
  private bool parseBeispielRegel() {
    if( tokenStream.peek() instanceof ConstToken ) {
      tokenStream.remove();
      if( tokenStream.peek() instanceof ConstToken ) {
        tokenStream.remove();
        while( tokenStream.peek() instanceof VarToken ) {
          tokenStream.remove();
        }
        return true;
      }
      else {
        // kein 2. const gefunden
        errorMessage = "Const expected";
        return false;
      }
    }
    else {
      // kein 1. const gefunden
      errorMessage = "Const expected";
      return false;
    }
  }



Einleitende Aufgabe zur Aufgabe 1 und 2 für’s Praktikum:
Wir schreiben zuerst einen Interpreter, also eine Parser, der gleich die Ausdrücke interpretiert und die Werte ausrechnet und als Rückgabewert der “Regel-Funktionen” zurückgibt.
Abstrakter Syntaxbaum
Auf Wikipedia findet schon einmal eine Definition: [[wikipdia:Abstract_syntax_tree#Abstract Syntax Tree]].
Ziel der Teilaufgaben d), e) und f) ist es, anstatt die Werte direkt auszuwerten, eine Baumstruktur zu benutzen um die Struktur des geparsten Textes zu speichern. Dieser kann dann getrennt (siehe Aufgabe 2) ausgewertet werden und wir brauchen ihn nur einmal zu parsen, selbst wenn wir verschiedene Operationen auf einem Ausdruck ausführen wollen – z.B. den Wert berechnen oder feststellen, welche Variablen er braucht, etc..
Was für Knotentypen kann dieser Baum haben?
Hinweis »
Man schaue sich Bild vom Ableitungsbaum oben an und frage sich, was man alles braucht um die gesamte Struktur (also alle Informationen) zu erfassen..

Antwort »
Wir brauchen einen Knotentyp für jede Operation (+, *, -, /) und natürlich auch für die Werte und Variablen.

In der Teilaufgabe d) sollen diese Klassen mit den entsprechenden Attributen und Methoden implementiert werden. Wir implementieren wieder ein Interface – nämlich IArithmetic – um eine Baumstruktur zu ermöglichen.
Dazu möchte ich auf Composite Pattern verweisen´, damit man versteht, welche Idee dahinter steckt.
Tree Walker
Bei der Aufgabe 2 geht es darum, einen mit dem Parser erstellten Evaluationsbaum zudurchlaufen und die Ausdrücke auszuwerten um den Wert des gesamtem Ausdruckes zu bestimmen. Dazu fügen wir eine Methode public int evaluate() zum Interface IArithmetic hinzu und implementieren sie dann für jeden Knotentyp derart, dass der Knotentyp seine Teilausdrücke auswertet und seine Operation darauf anwendet (falls er Teilausdrücke hat und ein Operator ist :D).
Dank Polymorphie und dem Composite Pattern geht das relativ schmerzlos.
Zusatzaufgabe (oder alternative Aufgabe)
Statt das Interface nachträglich zu ändern, kann man ein anderes, ebenfalls sehr mächtiges Design Pattern benutzen: das Visitor Pattern´ .
Damit können wir beliebig Operationen auf dem ganzen Baum definieren (wie das Auswerten oder Variablen bestimmen, etc.) ohne mehr als einmal das Interface und die Knotentypen anpassen zu müssen.
Das ist aber wirklich nur eine Zusatzaufgabe, falls noch Zeit bleibt.
Falls ich aber noch Zeit finde, werde ich auch noch Lösungen für alle Aufgaben in ANTLR entwickeln – es dürften nicht mehr als 100 Zeilen sein, aber mein ANTLR-Wissen ist etwas eingerostet..
Grüße,

Andreas
						Tags: ANTLR, Blatt 12, Composite Pattern, Exceptions, Lexer, Parser, Vistor Pattern
			            
			Filed in Aufgaben, Off-Topic, Tutorübung, Zur Vorlesung with 0 Comments 

					12 Dec 08 Heuristiken zum Aufgabenlösen     

			Frisch aus der Übung von heute die Zusammenfassung der Heuristiken:

Die Aufgebenstellung immer mehrmals lesen um sie auch wirklich voll zu erfassen
Sich selbst Fragen zum Problem stellen und diese beantworten (dadurch kann man das Problem auch besser erfassen)
Das Problem für Beispiele per Hand lösen
Teilprobleme suchen und lösen
Skizzen anfertigen
Das Problem anders beschreiben:

mit anderen Worten beschreiben
Definitionen anwenden
ein “mathematisches Modell” entwickeln (also versuchen das Problem mathematisch zu beschreiben)


ein leichteres Problem (eine Vereinfachung) zuerst lösen und dann auf das schwerere Problem verallgemeinern
Sonderfälle suchen und untersuchen

(z.B. sind oft die Sonder-/Extremfälle eines Problems gerade die Basisfälle eines rekursiven Lösungsansatzes

Meistens hilft wiederholtes Anwenden/Iteration und auch die Kombination solcher Ansätze um auf die Lösung zu stoßen.
						Tags: Probleme lösen
			            
			Filed in Off-Topic, Zur Vorlesung with 0 Comments 

					28 Nov 08 Rekursive Funktionen     

			Wie in der Übung versprochen ein Post über rekursive Funktionen.
Rekursive Funktionen sind Funktionen, die sich selbst aufrufen, und sind besonders in der funktionalen Programmierung das Mittel um Programme zu schreiben, da in der reinen funktionalen Programmierung keine Side Effects existieren.
Man kann generell rekursive Funktionen in zwei Klassen einteilen:

terminierende rekursive Funktionen
nicht-terminierende rekursive Funktionen

Wir wollen uns natürlich auf die terminierenden Funktionen beschränken, wobei es unmöglich ist vorab festzustellen, ob eine beliebige Funktion für alle Eingaben terminiert oder nicht (siehe Halte-Problem in der Theoretischen Informatik).
Deswegen möchte ich vorstellen, wie wir rekursive Funktionen schreiben können, die auch sicher terminieren und das machen, was wir wollen.
An sich ist es eine Art Schema F, aber trotzdem tut man sich am Anfang schwer damit, bis man richtig ‘reinkommt.
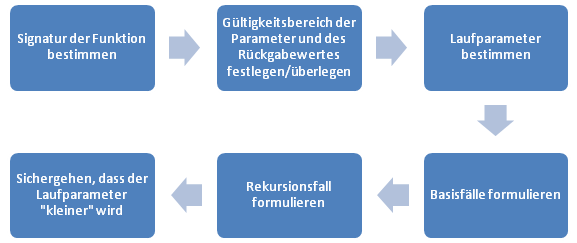
Das Schema F
Eine rekursive Funktion muss immer mindestens einen Parameter haben, der sich bei jeder Iteration einer Schranke (z.B. 0) weiter nähert und die Funktion terminiert genau dann, wenn diese Schranke getroffen wird, d.h. alle rekursiven Aufrufe übergeben einen kleineren Wert für diesen Parameter. Diesen Parameter will ich ab jetzt als Laufparameter oder Iterationsparameter bezeichnen.
Der kursiv geschriebene Teil ist besonders wichtig, denn daran erkennen wir sofort, ob eine rekursive Funktion sich daran hält und wir wissen auch, wie wir dies selbst bewerkstelligen können.
Beispiel:
int fib( int n ) {
  ensure( n >= 0 );

  if( n <= 1 ) {
    return n;
  else /* n >= 2 => n - 1, n - 2 >= 0 */
    return fib( n - 1 ) + fib( n - 2 );
}

Hier ist $$\text{n}$$ der Laufparameter und wie man sieht wird er bei jedem rekursiven Aufruf kleiner und nähert sich 0´ und bleibt auch immer $$ \ge 0 $$ (siehe Kommentar). Im Fall $$ n = 0 $$ wird die Rekursion beendet.
Bei einer Rekursion wird also die Ausführung auf Basisfälle zurückgeführt. Die Basisfälle der Fibonacci-Folge sind 0 und 1.
Frage: Wieso haben wir zwei Basisfälle?^Antwort
Ich habe auch ensure verwendet um sicherzustellen, dass die Funktion nur mit gültigen Werten für n aufgerufen wird. Dadurch stelle ich sicher, dass sie immer terminiert.
Man kann hier schon unser Schema heraus folgern:
Schema F für Rekursionen
Besonders bei rekursive definierten Folgen in der Mathematik lässt sich diese Schema ganz von selbst anwenden´.
Als ein Beispiel können wir die Berechnung der folgenden Folge betrachten:
$$

a_n := \begin{cases}

0 & \text{ : } n=0  \\

a_{n-1} – 2n – 1& \text{ : } n \ge 1

\end{cases}

$$
Die Signatur der Funktion in FJava ist offensichtlich $$\text{int a( int n )}$$.

Als Laufparameter kommt nur $$\text{n}$$ in Frage, einen anderen Parameter gibt es ja nicht.

Der Basisfall ist mit $$n=0$$ klar und die Rekursion erfolgt dann analog zur Definition und der Laufparameter wird mit $$\text{n-1}$$ auch kleiner, “geht also gegen 0” 
Nun zum Code:
int a( int n ) {
  ensure( n >= 0 );
  if( n == 0 )
    return 0;
  else
    return a( n - 1 ) + 2*n - 1;
}

Frage: Was berechnet diese Folge/Funktion?^Antwort
Rekursive Funktionen über Sequenzen
Ist der Laufparameter eine Sequenz, dann betrachten wir die Länge der Sequenz implizit als Laufparameter und müssen als Basisfall eine Sequenz der Länge $$n_0$$ benutzen. Meistens wählt man $$n_0 := 0$$ und prüft dann einfach, ob die Sequenz leer ist.

Manchmal weiß man aber, dass nur nicht-leere Sequenzen übergeben werden können oder Sequenzen einer Mindestlänge, dann müssen wir die Länge der Sequenz abfragen.
Beispiel:
<T> T last( Seq<T> seq ) {
  ensure( !isEmpty( seq ), "seq muss mindestens ein Element enthalten" );
  if( isEmpty(rest( seq )) ) // ist äquivalent zu: length( seq ) == 1
    return first(seq);

  return last(rest( seq ));
}

Man kann natürlich noch zusätzliche Basisfälle definieren – das kommt auf den Algorithmus an – aber man braucht mindestens einen Basisfall, damit die rekursive Funktion terminiert.´
Rückgabewerte im Basisfall
Oft ist der Basisfall eigentlich der Fall, in dem die Funktion nichts “tun” und der Wert des Ergebnisses vom Basisfall nicht beeinflusst werden soll.
Beispiele:
<T> int length( Seq<T> seq ) {
  if( isEmpty( seq ) )
    return 0;

  return 1 + length( rest( seq ) );
}

// gib jedes 2. Element zurück
// wir fangen an bei 0 zu zählen, wie bei Indizes üblich
<T> Seq<T> oddElements( Seq<T> seq ) {
  if( isEmpty( seq ) || isEmpty( rest( seq ) ) )
    return emptySeq();

  return concat( cons( first( rest( seq ) ) ), oddElements( rest( rest( seq ) ) ) );
}

/*
Testausgabe:
oddElements( cons( 0,1,2,3,4,5 ) )

[1, 3, 5]
*/

Was haben 0 und emptySeq() gemeinsam? Sie beeinflussen den Wert des Ergebnisses nicht.

Würden wir nicht addieren und konkatenieren, sondern im rekursiven Schritt multiplizieren, dann wäre unser Rückgabewert im Basisfall $$1$$.
Mathematische Begründung:

Alle Rückgabewerte im Basisfall waren neutrale Elemente ihrer jeweiligen Algebraischen Struktur über der Sorte und dem Operator, auf der im rekursiven Schritt operiert wurde.

In den Beispielen waren dies die Gruppen $$\left( \mathbb{Z}, + \right)$$ und $$\left( \mathrm{Seq}, \circ \right)$$.
Hieraus können wir auch noch eine Einsicht gewinnen:

Man kann keinen passenden Rückgabewert finden, der das Ergebnis nicht beeinflusst, wenn man zum Beispiel im rekursiven Schritt mit dem Rückgabewert addiert und multipliziert.
Rekursiv Denken
An sich sind wir jetzt mit allem technischen durch – das einzige, das noch fehlt, sind ein paar Anmerkungen, die einem helfen können, rekursive Funktionen zu erstellen. Dies folgt jetzt.
Rekursives Programmieren ist die Mutter aller Divide & Conquer-Strategien: man spaltet das Problem immer wieder in gleichartige Teilprobleme, mit deren Lösung man das ursprüngliche Problem lösen kann, auf, bis man ein “Basisproblem”´ erhält, das leicht zu lösen ist´.
Die meisten Rekursionen, die wir bisher programmiert haben, waren sehr “unbalanciert”:

Bei Sequenzen zum Beispiel teilen wir die Sequenz oft in das erste Element und den Rest auf und bearbeiten dann das Element direkt und lassen in der Rekursion die Funktion das Problem für den Rest der Sequenz lösen und setzen dann alles wieder zusammen – siehe length oder so gut wie alle Funktionen, die wir bisher geschrieben haben.
 length( cons( "a","b","c","d" ) ) schematisch dargestellt
Wenn wir also rekursive Funktionen auf Sequenzen schreiben, müssen wir uns immer überlegen, wie wir mit der Lösung für ein Teilsequenz unserer Eingabesequenz und direktem Zugriff auf ein oder zwei Elemente, die Lösung des Problems für die ganze Sequenz finden.
Dies ist der Grundgedanke der meisten Aufgaben, die wir behandeln.
Hilfsfunktionen
Oft hilft es auch, zusätzliche Hilfsfunktionen zu definieren, die einem die Arbeit erleichtern oder erst möglich machen, wenn die Signatur der Funktion selber nämlich keine Rekursion zulässt.
Als Beispiel die Tower-Funktion´:
// berechnet n^(n^(...)) n-mal Potenzieren (wobei ^ für's Potenzieren steht - deswegen heißt sie Turmfunktion)
int tower( int n ) {
  ensure( n >= 0 );
  return _tower( n, n );
}

int _tower( int n, int k ) {
  ensure( k >= 0 );
  if( k == 0 )
    return 1;

  return pow( n, _tower( n, k - 1 ) );
}

int pow( int a, int n ) {
  ensure( n >= 0 );
  if( n == 0 )
    return 1;

  return a * pow( a, n - 1 );
}

Hier brauchen wir einige Hilfsfunktionen, wobei auffallen sollte, dass die eigentliche tower Funktion nur ein Stub (eng. für Stummel) ist und _tower die eigentliche Arbeit erledigt.
Also wenn man nicht wirklich weiter kommt:

Einfach schauen, ob man vielleicht Hilfsfunktionen geschickt benutzen kann.
Soweit zur Theorie – im nächsten Post habe ich ziemlich viele Aufgaben gesammelt, die man ohne weiteres lösen kann ´.
						Tags: Divide-and-Conquer Strategien, FJava, rekursive Funktionen
			            
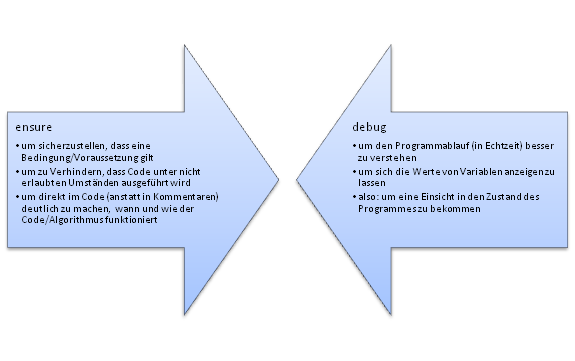
			Filed in Zur Vorlesung with 0 Comments 

					26 Nov 08 Ein paar Worte zu ensure und debug…     

			Das Merkblatt zu FJava sollte sich ja jeder ausdrucken und unters Kopfkissen legen und möglichst auch verstehen, aber ich möchte heute die Aufmerksamkeit auf die Sektion “Hilfsfunktionen” lenken.
Es werden zwei überaus nützliche Funktionen besprochen: ensure() und debug(), die außerdem für zwei klassische Hilfsmittel beim Programmieren stehen´.
debug()
debug kann man dazu verwenden um während der Ausführung etwas auszugeben. Der Name stammt vom Englischen to debug und wird in der Informatik verwendet um den Prozess der Fehlersuche und –korrektur in einem Computerprogramm, das nicht so läuft wie es soll, zu bezeichnen.
Die Ausgabe von Hilfsinformationen während das Programm läuft ist zugleich die älteste und die universellste Art Fehler zu suchen und den Ablauf des Programmes zu verfolgen. Praktisch alle Programmiersprachen und Systeme unterstützen eine Ausgabe von Daten zum Debuggen und der Programmierer ist frei in der Art und Weise, wann und wo er solche zusätzlichen Ausgaben hinzufügt.
Später im Verlauf der Vorlesung werden wir sicher noch weitere und mächtigere Mittel kennenlernen, die einem die Fehlersuche erleichtern, aber diese Mittel sind dann im Allgemeinen spezieller und aufwändiger.
Im Merkblatt wird im Beispiel kurz darauf eingegangen, wie man auch Variablen ausgibt, aber man kann auch beliebigen Ausrücken ausgeben.
debug( seq );

debug( "seq: " + seq );

debug( "first(seq): " + first(seq) );

Falls der Code nicht so funktioniert, wie er soll, und man die Ursache durch Lesen des Codes findet, kann man einfach in die Funktion ein paar debug()-Aufrufe einstreuen und sich dann beim Ablauf anschauen, wie sich die Werte verändern – dies ist besonders bei rekursiven Funktionen nützlich.
ensure()
ensure ist ein anderes sehr mächtiges Werkzeug, das von der Idee auch bei der Programmverifikation eingesetzt wird. In den meisten Programmiersprachen wird die Anweisung mit assert bezeichnet, aber ensure ist vom Sinn genauso verständlich. ensure stellt sicher, dass eine Bedingung zur Laufzeit gilt, ansonsten wird eine Fehlermeldung ausgegeben.
Man kann ensure benutzen um einerseits seinen Code gegen “falsche” Aufrufe zu sichern, als Beispiel:
int sub(int a, int b) {
 ensure( b >= 0 );
 if( b == 0 ) {
   return a;
 }
 else {
   return sub(a, b - 1) - 1;
 }
}

Ohne ensure könnte man sub(1, -1) aufrufen und das Programm würde in einer Endlosrekursion abstürzen ohne das man eine Ahnung hat wieso – in diesem Beispiel ist es noch einfach, aber spätestens bei größeren Funktionen, die sich gegenseitig aufrufen, kann’s unangenehm werden.
Man kann hier ensure benutzen um seinen Code gegen Missstände von außen abzusichern und gleichzeitig um deutlich zu machen, unter welchen Bedingungen man erwarten kann, dass die Funktion funktioniert 
Ein Vorteil von ensure gegenüber einfachen Kommentaren im Quellcode ist, dass ensure eine Anweisung ist, die auch ausgeführt wird und deswegen auch immer aktuell ist – im Gegensatz zu Kommentaren, die schon mal veraltet sein können..
Auch bei ensure kann man wieder eine Fehlermeldung ausgeben, die man selbst wählen kann – mit den gleichen Mittel wie bei debug:
ensure( !isEmpty( seq ), "Sequenz darf nicht leer sein!" );

ensure( i > 5, "i > " + i );

ensure( first(seq) > 0, "first(seq): " + first(seq) + " > 0" );

Man kann aber auch nur die Bedingung in ensure beschreiben und den Text weglassen:
ensure( true );

ensure( i > 0);

ensure( first(seq) > 0 );

Noch ein Beispiel zur “Programmverifikation”:
int sub(int a, int b) {
 ensure( b >= 0 );
 if( b == 0 ) {
   return a;
 }
 else {
   final int result = sub(a, b - 1) - 1;
   ensure( result == a - b );
   return result;
 }
}

Damit kann man bei jedem Aufruf sicherstellen, dass sub auch wirklich subtrahiert. Das ist natürlich kein Beweis für die Korrektheit der Funktion oder auch nur richtige Programmverifikation, aber es reicht auf jeden Fall aus um auch bei komplizierteren Funktionen zu testen, ob die Funktion sich in den Testfällen verhält, wie erwartet – weiterführend in dieser Richtung ist der Ansatz Design by Contract, bei dem bei jeder Funktion genau die Vor- und Nachbedingungen festgelegt werden (siehe oben die ensure-Bedingungen bei sub).
Also…
debug ist nützlich, wenn man das Programm besser verstehen will und/oder die Fehlerstelle einkreisen will. ensure kann man beim Entwickeln und allgemein nutzen um sicherzustellen, dass bestimmte Bedingungen zur Laufzeit erfüllt sind.

Die beiden Konzepte sind nicht orthogonal zu einander, aber man zumindest sagen, dass debug eher verwendet wird, wenn man Fehler sucht und zusätzliche Informationen braucht (also beim Testen und Debuggen) und ensure schon beim Schreiben des Codes eingesetzt wird um die Absichten des Autors einerseits und Beschränkungen des Codes andererseits deutlicher zu kennzeichnen.

Wie immer sind Kommentare und Feedback erwünscht 
Grüße,

Andreas
						Tags: assert, debug, debugging, design by contract, self-documenting code
			            
			Filed in Zur Vorlesung with 0 Comments 

					22 Nov 08 Kontext-freie Grammatiken     

			Ein paar Worte zu Beginn..
Beim Korrigieren der Hausaufgaben ist mir aufgefallen, dass möglicherweise das Konzept der (kontext-freien) Grammatiken noch nicht zur Ganzheit verstanden wurde, bzw. die Ausdrucksmöglichkeiten noch nicht vollständig erfasst wurden. Natürlich gehört auch Übung und auch ein gewisses Maß an Intuition dazu um “gute” Grammatiken zu schreiben, aber im Folgenden möchte ich versuchen ein paar Hinweise und Tipps zu geben´.
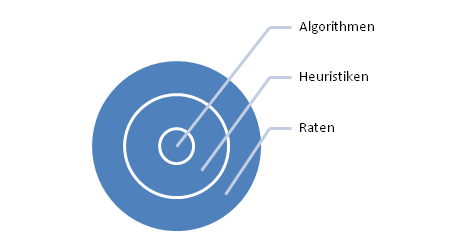
Zuerst möchte ich kurz auf das Konzept von Heuristiken im Software Engineering und in der Informatik allgemein eingehen´:

Heuristiken sind eine Verallgemeinerung von Algorithmen, dadurch gekennzeichnet, dass sie nicht so exakt und präzise formuliert sein müssen wie diese und auch nicht unbedingt immer funktionieren.

Heuristiken sind also “$$\pi$$ mal Daumen”-Ansätze und Regeln um oft gute Lösungen für ein Problem oder ähnliches zu finden, aber auch gleichzeitig Kompromisse.

Grammatiken
Betrachten wir nun ein paar “gute” Grammatiken und versuchen daraus Heuristiken abzuleiten.
Als erstes hätten wir die Grammatik aus der Hausaufgabe vom 2. Übungsblatt:
<bool_expr> ::= <bool_term> { “||” <bool_term> }*

<bool_term> ::= <bool_not> { “&&” <bool_not> }*

<bool_not> ::= [ ‘!’ ] <bool_factor>

<bool_factor> ::= <bool_const> | <bool_var> | ‘(‘ <bool_expr> ‘)’

<bool_const> ::= “true” | “false”

<bool_var> ::= ‘X’ | ‘Y’ | ‘Z’
Schon aus dieser Grammatik kann man ein paar Beobachtungen herleiten, die einem helfen zu bestimmen, ob eine Grammatik “gut” ist oder nicht:

Die Grammatik ist eindeutig, d.h. es gibt nur genau einen Ableitungsbaum für jedes Wort der Sprache, welche die Grammatik darstellt.
Jeder Operator kommt nur einmal in der Grammatik vor.
Die Struktur der Grammatik ist einfach (sequentiell) und ähnelt dem Schema des Operatorvorranges´.
Die geforderte Rekursion tritt nur an einer Stelle auf´.

Die Eindeutigkeit ist besonders wichtig, wenn wir daran denken, für wen solche Grammatiken gemeinhin gedacht sind: Computer/-programme. Programme oder Unterprogramme, die aus einem Ausdruck einen Ableitungsbaum konstruieren, heißen übrigens Parser´.

Eindeutigkeit ist also sicherlich eine Eigenschaft, die wünschenswert ist, wenn wir versuchen einen Ableitungsbaum zu erstellen. Erstellen wir einen Ableitungsbaum müssen wir ja rückwärts vorgehen und versuchen aus den einzelnen Grundelementen, die wir zur Verfügung haben, die Regeln abzuleiten, aus denen sie erzeugt wurden, und aus diesen dann ihre “Elternregeln”, usw. bis wir die Startregel erreichen.
Eindeutigkeit
Wie stellt man nun Eindeutigkeit sicher?
Wir können festlegen:
Zwei fortgeschrittene, verschiedene Ketten von Regelersetzungen (denn Grammatiken definieren ja nichts anderes als Termersetzungen, bei denen auf der rechten Seite immer nur genau ein Nicht-Terminal steht) enden in verschiedenen Wörtern der formalen Sprache (wenn sie überhaupt terminieren)´.
Oder anders gesagt:

Jedes Wort der formalen Sprache besitzt genau einen Ableitungsbaum (Äquivalenz durch Kontraposition).
Die Idee hier ist, dass man Grammatiken nicht nur benutzen kann, um aus vorgegebenen Ausdrücken Ableitungsbäume o.ä. zu konstruieren, sondern auch um neue Ausdrücke zu bauen (wieder analog zu den Konzepten von Termersetzungen, Grundtermen und Normalformen – Quizfrage: was sind hier die Analogien zu Grundformen und Normalformen?).
Als Beispiel (mit der Grammatik aus der Hausaufgabe):
<bool_expr> –> <bool_term> || <bool_term> –> <bool_not> || <bool_term> –> <bool_factor> || <bool_term> –> … –> X | Y
Aber zurück zum Thema: was ist nicht eindeutig?
Betrachten wir:
<startRegel> ::= <regelA> “||” <regelA> | <regelB> “||” <regelB>

.

.

.
Über diese Grammatik können wir keine Aussage bzgl. der Eindeutigkeit machen!

Der Fall, der uns interessiert ist folgender (als Beispiel):
<startRegel> ::= <regelA> | <regelB>

<regelA> ::= <regelC> “||” <regelC>

<regelB> ::= <regelC> “||” <regelC>
Man sieht leicht, dass wir es hier mit einer nicht eindeutigen Grammatik zu tun haben.

Aber genauso wenig eindeutig ist:
<startRegel> ::= <regelA> | <regelB>

<regelA> ::= <regelC> {“||” <regelC>} *

<regelB> ::= <regelC> {“||” <regelC>} +
Oder:
<regelA> ::= <regelA> + <regelA> | <regelA>  − <regelA> | <regelA>
(Wieso?)
Worauf ich hinaus will: man kann wohl beliebig komplizierte/nicht-triviale Grammatiken bauen, die nicht eindeutig sind.
Wir kommen also mit dieser Eigenschaft nicht wirklich weiter, außer dass wir sagen können, dass sie wünschenswert ist. Als Heuristik ist sie aber insgesamt tauglich, weil wir sagen können, dass die Eindeutigkeit das große Ziel ist, wonach wir streben, wenn wir Grammatiken schreiben (mit den richtigen Techniken/Vorgehensweisen folgt sie aber fast automatisch).
Das heißt:

Es ist also gut zu versuchen, die Grammatik nicht mehrdeutig werden zu lassen, denn wenn man versucht eindeutige Grammatiken zu schreiben, erhält man automatisch  auch einfache/knappe Grammatiken, was auf jeden Fall gut ist.
Semantische Eindeutigkeit
Betrachten wir also nun die 2. Eigenschaft: “Jeder Operator kommt nur einmal vor in der Grammatik vor.”

Die Beobachtung hierbei ist, dass es sinnvoll ist, jeden Operator nur einmal in einer Regel zu beschreiben, denn dann ist klar, dass zumindest dieser Operator eindeutig durch genau eine Regel gematcht (oder von ihr erzeugt) werden kann.
Wir können diese Beobachtung noch allgemeiner fassen, wenn wir uns kurz von dem Beispiel der booleschen Ausdrücke entfernen.
<ifexpr> ::= “if(” <cond> “)” <cmdblock> { “else” <cmdblock> }

<cmdblock> ::= <ifOrCmd> | [ ‘{‘ <ifOrCmd> {<ifOrCmd>}* ‘}’ ]

<ifOrCmd> ::= <command> | <ifexpr>
Hier haben wir es nicht mehr wirklich mit Operatoren zu tun, dafür aber mit if-Anweisungen. Man kann aber auch hier etwas feststellen:

jede Regel behandelt genau ein semantisches Konzept´.
Die Bezeichnung “semantisches Konzept” versucht auszudrücken, dass es sich um ein abstraktes Konzept handelt, das Teil der Sprache ist, und dass wir die Konzepte nach ihrer Semantik, also ihrer Bedeutung, unterscheiden.

Diese Feinheit ist insbesondere dann wichtig, wenn wir Sprachen betrachten, bei denen verschiedene Konzepte mit unterschiedlicher Bedeutung die gleiche Syntax haben.

Das ist jetzt nicht an den Haaren herbeigezogen, sondern es gibt sogar sehr viele Programmiersprachen, bei denen diese Unterscheidung wichtig ist. Als Beispiel sei hier nur Visual Basic angegeben.
In Visual Basic wird Variablen mit = ein Wert zugewiesen, andererseits wird in Bedingungen auch mit = überprüft, ob zwei Variablen den gleichen Wert haben. Natürlich ist es dann auch wahrscheinlich, dass es Probleme mit der Eindeutigkeit gibt; diese werden aber durch geschickte Wahl der Regeln oder Kontextbedingungen (siehe Vorlesung) umgangen.
Als Gegenbeispiel, dass diese Eigenschaft nicht immer erfüllt ist, betrachten wir dazu einmal einen Ausschnitt der Sprache Java aus den offiziellen Spezifikationen:
IfThenStatement:

if ( Expression ) Statement
IfThenElseStatement:

if ( Expression ) StatementNoShortIf else Statement
IfThenElseStatementNoShortIf:

if ( Expression ) StatementNoShortIf else StatementNoShortIf
Expression:

“ein boolescher Ausdruck”
Statement:

“eine beliebige weitere Anweisung (auch IfThenStatement und IfThenElseStatement)”
StatementNoShortIf:

“eine beliebige weitere Anweisung (aber nur IfThenElseStatementNoShortIf und nicht IfThenStatement oder IfThenElseStatement)”
Ohne weiter auf den tieferliegenden Grund einzugehen (näheres dazu findet sich in den Spezifikationen) kann man aber feststellen, dass hier ein semantisches Konzept – die if-else-Anweisung – in mehr als einer Regel behandelt wird. D.h. die Beobachtung über die semantischen Konzepte ist auch höchstens eine Heuristik um eine gute Grammatik zu konstruieren und man muss auch daran denken, dass die Unterteilung nicht immer ganz klar ist.

Als Beleg dafür, dass sie trotzdem eine sehr nützliche Heuristik ist, sei auf die Übung 3 im 2. Übungsblatt verwiesen:
<table> ::= “<table” {<border>} “>” <headerRow> {<rows>}* “</table>”

<border> ::= “border=\”” <number> “\””

<headerRow> ::= “<tr>” {<headerData>}* “</tr>”

<headerData> ::= “<th>” <data> “</th>”

<rows> ::= “<tr>” {<rowData>}* “</tr>”

<rowData> ::= “<td>” <data> “</td>”

<data> ::= <table> | <number> | <text>

<number> ::= [ <ziffer> {<ziffer> | ‘0’}* ] | ‘0’

<ziffer> ::= ‘1’ | ‘2’ | ‘3’ | ‘4’ | ‘5’ | ‘6’ | ‘7’ | ‘8’ | ‘9’

<text> ::= {‘a’ | ‘b’ | ‘c’ | … | ‘z’ | ‘A’ | ‘B’ | … | ‘Z’}+
Struktur der Grammatik
Aus den bisher angegebenen Grammatiken kann man auch noch zwei weitere wichtige Heuristiken herleiten. Vorher schauen wir uns aber zuerst noch die 3. Eigenschaft vom Anfang an: “Die Struktur der Grammatik ist einfach (sequentiell) und ähnelt dem Schema des Operatorvorrang.”
Zuerst einmal: was ist damit gemeint?
Beide Teilaussagen der Eigenschaft werden hoffentlich klar(er), wenn man folgende Hierarchie anschaut:

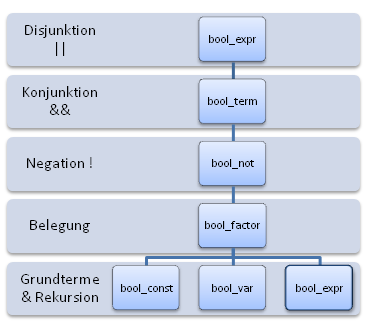
Erinnern wir uns jetzt, dass bei der Aufgabe folgender Operatorvorrang gelten soll (vom schwächeren zum stärker bindenden Operator hin):

Dann ist klar, dass Operatorvorrang und Regelhierarchie übereinstimmen und dies ist auch allgemein so:

Damit kann man schon recht leicht “nach Schema F” beliebige Rechenstrukturen mit beliebigen Operatorpräzedenzen/-vorrang abarbeiten und in eine Grammatik umwandeln, es stellt sich nur die Frage, wie es bei anderen Sprachkonstrukten aussieht.
Auf jeden Fall können wir noch ein anderes Ergebnis zusammenfassen, das bisher in allen Lösungen und Beispiele sichtbar war und auch so in der 3. Eigenschaft formuliert ist:

Es ist also sinnvoll, dass wir immer versuchen, die Regeln so einfach wie möglich zu formulieren, weil dies bei den Sprachen, die man normalerweise behandelt auch möglich ist. (Entweder das, oder es gibt gar keine Darstellung der Sprache als kontext-freie Grammatik – siehe dazu die Aufgabe 4 des 2. Übungsblattes mit der Frage, ob es eine BNF-Beschreibung der Sprache $$a^nb^nc^n$$ gibt.)
Insbesondere gibt uns das auch noch einen Hinweis, wie weit man die semantischen Konzepte versucht zu vereinfachen und zwar: so weit wie möglich. D.h. lieber mehr einfach strukturierte Regeln als eine äußerst komplexe.
Rekursion
Als letztes noch die 4. Beobachtung: “Die geforderte Rekursion tritt nur an einer Stelle auf.”. Aus den Beispielen kann man sehen, dass die Rekursion meistens erst sehr weit “unten” in der Hierarchie auftritt.

Dadurch, dass man die Rekursion möglichst weit nach unten “drückt”, also in die Richtung der Grundterme hin, kann man leicht sicherstellen, dass die Rekursion möglichst allgemein gilt und gleichzeitig erübrigt sich dadurch eine weitere Behandlung der gleichen Rekursion in der Hierarchie darüber.
In der Vorlesung wurde auch noch erwähnt, dass sich kontext-freie Grammatiken besonders zur Darstellung von Klammerstrukturen eignen, indem man rekursive Regeln aufstellt. Die Grammatiken der Tabellen und auch die geklammerten booleschen Ausdrücke oben sind gute Beispiele dafür und auch für das “Herunterdrücken” des Rekursionsfalles.
Hierzu noch ein kleines Beispiel für eine Grammatik, die alle gültigen Datensorten in FJava beschreibt:
<BasisTyp> ::= “int” | “float” | …
<WrapperTyp> ::= “Integer” | “Float” | …

<SequenzTyp> ::= “Seq” “<” <ObjektTyp> “>”
<ObjektTyp> ::= <WrapperTyp> | <SequenzTyp>
<Typ> ::= <BasisTyp> | <ObjektTyp>
Wir fassen also zusammen:

Zusammenfassung und Ausblick
Damit haben wir fünf Heuristiken kennengelernt, die einem helfen können, bessere Grammatiken zu schreiben:

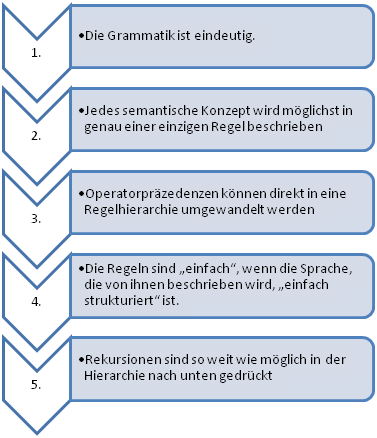
Zum Abschluss noch zwei zusätzliche Tipps, um sicherer im Umgang mit kontext-freien Grammatiken zu werden:

Üben, üben, üben! 

Wir haben Fjava in der Vorlesung nicht wirklich definiert, deswegen bietet es sich an für die Sprache selbst eine Grammatik zu entwerfen.

Es gibt aber auch Tools frei im Internet, mit denen man Parser aus einer BNF-ähnlichen Beschreibung einer Sprache erstellen kann. Es wäre also möglich die “Broy-Notation” aus der Vorlesung in Fjava umzuwandeln (mittels eines solchen Parsers und einfachen Textersetzungen). Wenn es dazu Fragen gibt, dann kann ich da gerne ein paar Links heraussuchen.
Es gibt viele Programmiersprachen und jede etwas ernsthaftere hat eine Spezifikation und alle beschreiben ihre Sprachen mittels einer Notation, die mehr oder weniger direkt auf der BNF-Notation basiert – man kann dort auch nach Inspirationen suchen 😉

Falls es noch Fragen gibt oder Feedback, dann schreibt mir eine Email oder nutzt die Kommentarfunktion ´
						Tags: BNF, Grammatik, Heuristik, Java
			            
			Filed in Zur Vorlesung with 0 Comments 

					14 Nov 08 Wann benutzt man $$\equiv$$ und wann $$\Leftrightarrow$$?     

			Bei der Korrektur der Hausaufgaben ist mir aufgefallen, dass viele $$\Leftrightarrow$$ statt $$\equiv$$ benutzen, wenn sie die logische Terme umformen. Die Musterlösungen verwenden immer $$\equiv$$, wie vielleicht aufgefallen ist, und ich habe das Verwenden von $$\Leftrightarrow$$ in der letzten Hausaufgabe auch immer angestrichen (aber keine Punkte abgezogen).

Deshalb ist es sinnvoll, einen kleinen Überblick zu geben, für den in der Übung heute keine Zeit war:
Also wann benutzt man was?
Wenn wir mit algebraischen Gleichungen der Form
$$ x^2 = 9 $$
arbeiten, benutzen wir $$\Leftrightarrow$$ um auszudrücken, dass bestimmte Gleichungen äquivalent sind, also unter den bekannten Umformungen semantisch gleich sind (u.a. für die Variable $$x$$). Als Beispiel:
$$\left.\begin{array}{cc}

&  x^2 = 9 \\

\Leftrightarrow & \left|x \right| = 3 \end{array}\right.$$
Während also $$+$$, $$-$$, $$*$$, etc. Operatoren sind auf die wir Umformungen anwenden, benutzen wir $$\Leftrightarrow$$, aber auch die anderen logischen Operatoren, als Metaoperatoren (meta: griech. ‘über’) um über die Gleichungen Aussagen zu machen (also dass sie äquivalent sind zum Beispiel).

Ein anderer Metaoperator wäre zum Beispiel $$\Rightarrow$$ bei algebraischen Gleichungen:
$$\left.\begin{array}{cc}

&  x = 3 \\

\Rightarrow& x^2 = 9 \end{array}\right.$$
In der Aussagen- und Prädikatenlogik operieren wir aber auf Aussage (bzw. Aussageformen) und dieses Mal sind die Metaoperatoren oben unsere Operatoren ($$\Leftrightarrow$$, $$\Rightarrow$$, etc.), d.h. wir brauchen andere Metaoperatoren um über die Aussagenlogik diskutieren zu können. $$\equiv$$ ist ein solcher Metaoperator, $$\not \equiv$$ auch und $$\models$$ ein anderer, den wir vielleicht später kennen lernen werden.

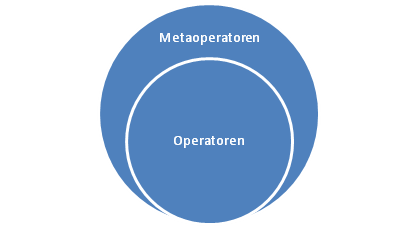
Wir benutzen $$\equiv$$ um etwas über die Gleichheit von Ausdrücken/Gleichungen der Aussagenlogik zu sagen.
$$\left.\begin{array}{ccccc}

&  x^2 = 9 &   & & \lnot a \Leftrightarrow  \lnot b  \\

\Leftrightarrow & \left|x \right| = 3 & \;\;\;\;\;\;\;\;\;\; & \equiv & a \Leftrightarrow b \end{array}\right.$$
In dieser Gegenüberstellung sieht man, wie $$\Leftrightarrow$$ rechts als normaler Operator auftritt und $$\equiv$$ als Metaoperator benutzt wird.
						Tags: Äquivalenz, Metaoperatoren, Operatoren
			            
			Filed in Zur Vorlesung with 0 Comments

28 Jan 09 Blatt 12 (Lexer und Parser)

Vorbereitung und Informationen zu den Aufgaben

Rekursiv-absteigende Parser

Lexer

Beispiel

Lexer, die zweite

Parser, die zweite

Einleitende Aufgabe zur Aufgabe 1 und 2 für’s Praktikum:

Abstrakter Syntaxbaum

Tree Walker

Zusatzaufgabe (oder alternative Aufgabe)

12 Dec 08 Heuristiken zum Aufgabenlösen

28 Nov 08 Rekursive Funktionen

Das Schema F

Rekursive Funktionen über Sequenzen

Rückgabewerte im Basisfall

Rekursiv Denken

Hilfsfunktionen

26 Nov 08 Ein paar Worte zu ensure und debug…

debug()

ensure()

Also…

22 Nov 08 Kontext-freie Grammatiken

Ein paar Worte zu Beginn..

Grammatiken

Eindeutigkeit

Semantische Eindeutigkeit

Struktur der Grammatik

Zuerst einmal: was ist damit gemeint?

Rekursion

Zusammenfassung und Ausblick

14 Nov 08 Wann benutzt man $$\equiv$$ und wann $$\Leftrightarrow$$?

Also wann benutzt man was?

Pages

Categories

Blogroll

Archives

Tags

Meta