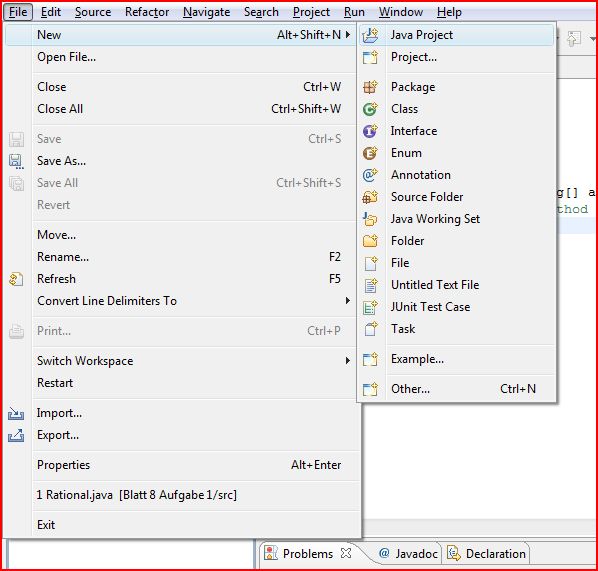
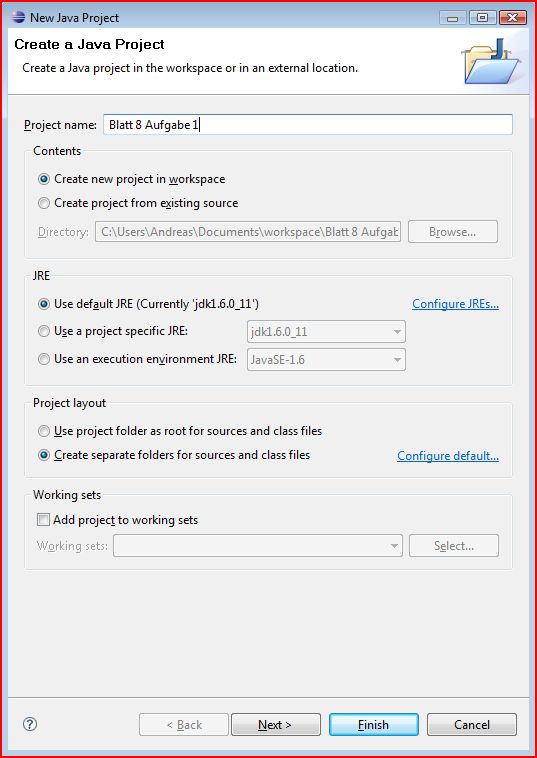
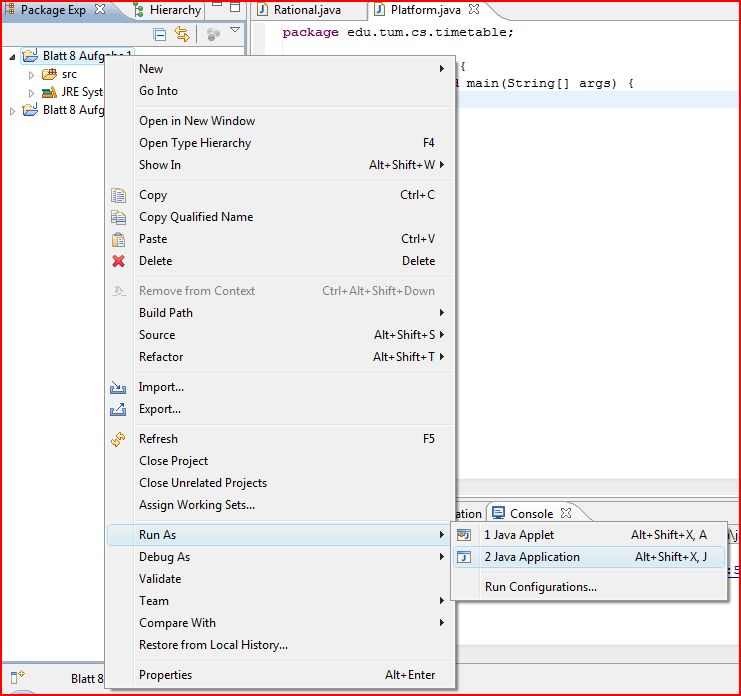
19 Dec 08 Blatt 8 – Eclipse Hilfen für den Anfang
Ein paar kleine Hilfsstellungen zum Einstieg, damit man vielleicht doch nicht ganz verloren ist:
12 Dec 08 Heuristiken zum Aufgabenlösen
Frisch aus der Übung von heute die Zusammenfassung der Heuristiken:
- Die Aufgebenstellung immer mehrmals lesen um sie auch wirklich voll zu erfassen
- Sich selbst Fragen zum Problem stellen und diese beantworten (dadurch kann man das Problem auch besser erfassen)
- Das Problem für Beispiele per Hand lösen
- Teilprobleme suchen und lösen
- Skizzen anfertigen
- Das Problem anders beschreiben:
- mit anderen Worten beschreiben
- Definitionen anwenden
- ein “mathematisches Modell” entwickeln (also versuchen das Problem mathematisch zu beschreiben)
- ein leichteres Problem (eine Vereinfachung) zuerst lösen und dann auf das schwerere Problem verallgemeinern
- Sonderfälle suchen und untersuchen
(z.B. sind oft die Sonder-/Extremfälle eines Problems gerade die Basisfälle eines rekursiven Lösungsansatzes
Meistens hilft wiederholtes Anwenden/Iteration und auch die Kombination solcher Ansätze um auf die Lösung zu stoßen.
Tags: Probleme lösen
12 Dec 08 Blatt 7 Aufgabe 3
Ein kleines “Gerüst” für die Aufgabe 3: aufgabe3.zip
Zusatzaufgabe:
d) Füge zuerst zu Lines eine Funktion hinzu
static void drawLine( double[][] image, double color,
double x1, double y1, double x2,
double y2, double width )
die eine Linie mit variabler Breite width zeichnet (linkes Teilbild unten) und dann eine Funktion
static void drawSmoothLine( double[][] image, double color,
double x1, double y1, double x2,
double y2, double width )
die analog zu drawLine eine weiche Line der Breite width einzeichnet. So wie die Linie auf dem rechten Teilbild:
)Tags: Anti-Aliasing, Aufgabe 3, Blatt 7
12 Dec 08 For Each-Schleifen Beispiel
Hier ein einfaches Beispiel für das for each Schleifen-Konstrukt in Java:
public class ForEachExample { public static void main(String[] args) { int[] feld = new int[] { 1,2,3,4 }; for ( int eintrag : feld ) { System.out.println( eintrag ); } } }Tags: Blatt 7
12 Dec 08 Wiederholung: Arrays
Eine kurze Übersicht der wichtigsten Array-Befehle:
Deklarieren einer Array-Referenz/Variable:
int[] integerArray; // allgemein: // T[] tArray; // T kann selbst wieder vom Typ Array sein, also T := U[] usw..Erstellen eines neuen Array-Objektes:
integerArray = new int[5]; // Erstellen eines neuen Array-Objektes: integerArray = new int[5]; // geht leider nicht!!! // integerArray = new int[3] { 3, 1, 4 }; // oder: integerArray = new int[] { 3, 1, 4, 1, 5, 6, 9 }; // wo ist der Fehler (Achtung: Scherzfrage)Zugriff auf ein Element in einem Array
System.out.println( integerArray[0] + "," + integerArray[1] + integerArray[2] + integerArray[3] + " ist ca. \pi" ); // Zuweisen eines Wertes analog: integerArray[5] = 9; integerArray[6] = 2; // besser, eh?Abfragen der Länge eines Arrays:
// mit .length System.out.println( "\pi auf " + integerArray.length + " - 1 Stellen genau:" ); // man indiziert mit int Variablen dynamisch: System.out.print( "\pi ~ " + integerArray[0] + "," ); // wir fangen jetzt ab der ersten Nachkommastelle an (also 2. Element im Array) for( int i = 1 ; i < integerArray.length ; i++ ) { System.out.print( integerArray[i] ); } System.out.println(); [/sourcecode]</pre> Überprüfung auf Gleichheit: <pre> // wie bei Strings mit .equals int[] arrayA = new int[] {1, 2, 3, 3}; int[] arrayB = new int[] {3, 2, 1}; int[] arrayC = new int[] {1, 2, 3, 4}; System.out.println( arrayA.equals( arrayA ) ); // true System.out.println( arrayA.equals( arrayB ) ); // false System.out.println( arrayA.equals( arrayC ) ); // falseCode: ArrayExample.java
Tags: Blatt 7
10 Dec 08 Aufgaben zur prozeduralen Programmierung (TODO)
Hier ein paar Übungsaufgabe zur prozeduralen Programmierung. Vorab kann ich aber nur empfehlen die Aufgaben aus dem Praktikum auch zu wiederholen und zwar so lange, bis man die Schleifen-Konstrukte im Schlaf beherrscht und die Aufgaben auch so kein Problem mehr darstellen.
Außerdem empfiehlt es sich generell zusätzlich zu Vorlesungen noch weitere Literatur zu benutzen, in unserem Falle also einerseits ein Buch zum theoretischen Teil der Vorlesung (es empfiehlt sich wahrscheinlich das Buch von Prof. Broy) und eines für Java, wobei da wohl jedes Java-Buch gleichermaßen geeignet ist.
Die andere Darstellung der Inhalte ist oft hilfreich und man bekommt ein besseres Gefühl für die Sprache selber – wobei natürlich das Schreiben von Java-Code die beste Möglichkeit ist um die Sprache zu lernen!Code Convention für Java
Diese Aufgabe wird wahrscheinlich noch in einen eigenen Blogeintag erweitert werden, aber insbesondere in Hinblick auf die Klausur (für die Korrektur) und die Tatsache, dass wir jetzt langsam richtig in die Programmierung einsteigen, möchte ich eine Link posten, der für Anfänger hilfreich sein sollte und auch für diejenigen, die schon mehr Java programmiert haben, interessant sein kann:
Code Conventions for the Java Programming Language
Hierbei handelt es sich um ein ziemlich ausführliches Handbuch, wie der Java-Code von Sun (den Erfindern von Java) formatiert werden soll.
Man kann sich über die genaue Formatierung von Code streiten (in einschlägigen Foren finden sich mehr als genügend Beispiele dafür), aber auf jeden Fall sollte der Quellcode, den man schreibt einheitlich formatiert werden und auf eine Art und Weise, die sowohl übersichtlich ist als auch der Syntax der Sprache gerecht wird.Beim jetzigen Stand in den Übungen kann ich das Kapitel 1 Introduction (ein sehr kurzer Text) und das Kapitel 7 Statements empfehlen.
Ich bin selber nicht mit allem einverstanden, was teilweise in den anderen Kapiteln steht, aber dieses Dokument ist ein guter Einstiegspunkt und gibt gute Hinweise darauf, wie man seinen Code formatieren sollte.Als generelle $$\pi$$ mal Daumen-Regel kann ich ansonsten nur sagen: “Jede Anweisung in ihrer eigenen Zeile.”
Aufgaben
Texthaus
Als Vorbeitung empfiehlt sich die Aufgabe 2 vom Übungsblatt 6.
Ziel der Aufgabe ist es eine Prozedur zu schreiben, die ein Haus als Text ausgibt:
x x x x x x x x x xxxxxxxxx x x x x x x x x xxxxxxxxx
- Schreibe eine Prozedur, die in Abhängigkeit von einem positiven Integer-Parameter n > 1 (Wieso?) ein Haus (in der obigen Form) der Breite n mit System.print() und System.println() zeichnet und auf der Konsole ausgibt.
Hinweise:
Für ungerade n ist das Haus oben ein Beispiel – wie sieht das Haus für gerade n aus? (Lösungsskizze!)
Zusätzlich- Damit das Haus besser isoliert ist, soll das Innere des Dachs mit ^ und die Hauswand mit # ausgefüllt werden.
Außerdem sind Hochhäuser in, deswegen wäre es schön, wenn das Haus mehrere Stockwerke haben könnte – man füge also eine Parameter m > 0 hinzu, der angibt, wie viele Stockwerke das Haus haben soll und zeichne das Haus entsprechend.Permutationen
Permutationen sind sehr leicht mit Schleifen zu erzeugen, deswegen:
Man schreibe eine Funktion <T> Seq<Seq<T>> getPermutations( Seq<T> set ), die alle Permutationen von set zurückgibt.
Hinweise:
Es lohnt sich auf jeden Fall die übliche Vorgehensweise zu probieren, selbst wenn die Aufgabe abschreckend wirkt:Ein paar einfache Beispiele per Hand lösen, dann schauen, wie man die Lösungen in Teilprobleme zerlegen kann (also wie man eine Permutation mit Hilfe von Teilpermutationen bestimmen kann).
Hierbei können (wie so oft sonst auch) kleine Skizzen nützlich sein.Achtung:
PS: Dieser Eintrag ist TODO, d.h. ich werde hier wahrscheinlich noch ein paar Dinge anfügen, nur wollte ich, weil ich momentan einiges um die Ohren habe und die Klausur ansteht, auch zumindest diese beiden kleinen Aufgaben nicht vorenthalten.
Feedback ist, wie immer, erwünscht.
05 Dec 08 Blatt 6 Folien
Anbei ein paar (die wichtigesten) Folien von der heutigen Übung.
(more…)05 Dec 08 Blatt 6, Aufgabe 3e
Hier noch eine etwas elegantere Lösung zur Aufgabe 3e:
// save as fib.java public class fib { static public int fib(int n) { int f_old = 1, f_current = 0; for( int i = 0 ; i < n ; i++ ) { int f_old_old = f_old; f_old = f_current; f_current = f_old_old + f_old; } return f_current; } static public void main( String[] args ) { // small test for( int i = 0 ; i < 10 ; i++ ) { System.out.println( fib(i) ); } } } [/sourcecode]Was ist der Trick?
Tags: Blatt 6, Fibonacci-Folge, iterativer Ansatz
05 Dec 08 Blatt 6, Aufgabe 1
Hier zuerst einmal das Grundgerüst aus dem Übungsblatt:
import fjava.Seq; import static fjava.Seq.*; @SuppressWarnings("unchecked") public class Program { static <T> void printSeq(Seq<T> s) { System.out.print(s); } public static void main(String[] args) { printSeq(cons(1,2,3,4)); } }Ich habe auch ein paar Batch-Dateien zusammengeschrieben um das Leben leichter zu machen – zumindest für die, die auch Windows benutzen:
compile.bat führt einfach den javac-Befehl aus dem Übungsblatt aus. Zum Beispiel: compile Program.java.
run.bat führt den java-Befehl aus: run Program.startCmd.bat startet Cmd (sowas wie xterm für Windows) im Verzeichnis, in dem sich die Datei befindet – das erspart einem herumnavigieren in der Shell.
setupPath.bat kann man benutzen, wenn die Shell javac/java nicht findet. Möglicherweise muss man den Pfad in der Datei anpassen (einfach mal in Notepad öffnen und sich anschauen..).
Tags: Blatt 6
28 Nov 08 Rekursive Funktionen
Wie in der Übung versprochen ein Post über rekursive Funktionen.
Rekursive Funktionen sind Funktionen, die sich selbst aufrufen, und sind besonders in der funktionalen Programmierung das Mittel um Programme zu schreiben, da in der reinen funktionalen Programmierung keine Side Effects existieren.
Man kann generell rekursive Funktionen in zwei Klassen einteilen:
- terminierende rekursive Funktionen
- nicht-terminierende rekursive Funktionen
Wir wollen uns natürlich auf die terminierenden Funktionen beschränken, wobei es unmöglich ist vorab festzustellen, ob eine beliebige Funktion für alle Eingaben terminiert oder nicht (siehe Halte-Problem in der Theoretischen Informatik).
Deswegen möchte ich vorstellen, wie wir rekursive Funktionen schreiben können, die auch sicher terminieren und das machen, was wir wollen.
An sich ist es eine Art Schema F, aber trotzdem tut man sich am Anfang schwer damit, bis man richtig ‘reinkommt.
Das Schema F
Eine rekursive Funktion muss immer mindestens einen Parameter haben, der sich bei jeder Iteration einer Schranke (z.B. 0) weiter nähert und die Funktion terminiert genau dann, wenn diese Schranke getroffen wird, d.h. alle rekursiven Aufrufe übergeben einen kleineren Wert für diesen Parameter. Diesen Parameter will ich ab jetzt als Laufparameter oder Iterationsparameter bezeichnen.
Der kursiv geschriebene Teil ist besonders wichtig, denn daran erkennen wir sofort, ob eine rekursive Funktion sich daran hält und wir wissen auch, wie wir dies selbst bewerkstelligen können.
Beispiel:
int fib( int n ) { ensure( n >= 0 ); if( n <= 1 ) { return n; else /* n >= 2 => n - 1, n - 2 >= 0 */ return fib( n - 1 ) + fib( n - 2 ); }Hier ist $$\text{n}$$ der Laufparameter und wie man sieht wird er bei jedem rekursiven Aufruf kleiner und nähert sich 0´ und bleibt auch immer $$ \ge 0 $$ (siehe Kommentar). Im Fall $$ n = 0 $$ wird die Rekursion beendet.
Bei einer Rekursion wird also die Ausführung auf Basisfälle zurückgeführt. Die Basisfälle der Fibonacci-Folge sind 0 und 1.
Frage: Wieso haben wir zwei Basisfälle?Antwort
Ich habe auch ensure verwendet um sicherzustellen, dass die Funktion nur mit gültigen Werten für n aufgerufen wird. Dadurch stelle ich sicher, dass sie immer terminiert.
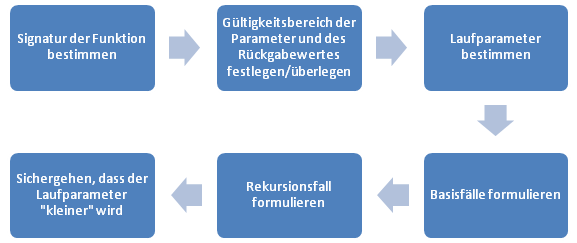
Man kann hier schon unser Schema heraus folgern:
Schema F für Rekursionen
Besonders bei rekursive definierten Folgen in der Mathematik lässt sich diese Schema ganz von selbst anwenden´.
Als ein Beispiel können wir die Berechnung der folgenden Folge betrachten:
$$
a_n := \begin{cases}
0 & \text{ : } n=0 \\
a_{n-1} – 2n – 1& \text{ : } n \ge 1
\end{cases}
$$Die Signatur der Funktion in FJava ist offensichtlich $$\text{int a( int n )}$$.
Als Laufparameter kommt nur $$\text{n}$$ in Frage, einen anderen Parameter gibt es ja nicht.
Der Basisfall ist mit $$n=0$$ klar und die Rekursion erfolgt dann analog zur Definition und der Laufparameter wird mit $$\text{n-1}$$ auch kleiner, “geht also gegen 0”Nun zum Code:
int a( int n ) { ensure( n >= 0 ); if( n == 0 ) return 0; else return a( n - 1 ) + 2*n - 1; }Frage: Was berechnet diese Folge/Funktion?Antwort
Rekursive Funktionen über Sequenzen
Ist der Laufparameter eine Sequenz, dann betrachten wir die Länge der Sequenz implizit als Laufparameter und müssen als Basisfall eine Sequenz der Länge $$n_0$$ benutzen. Meistens wählt man $$n_0 := 0$$ und prüft dann einfach, ob die Sequenz leer ist.
Manchmal weiß man aber, dass nur nicht-leere Sequenzen übergeben werden können oder Sequenzen einer Mindestlänge, dann müssen wir die Länge der Sequenz abfragen.Beispiel:
<T> T last( Seq<T> seq ) { ensure( !isEmpty( seq ), "seq muss mindestens ein Element enthalten" ); if( isEmpty(rest( seq )) ) // ist äquivalent zu: length( seq ) == 1 return first(seq); return last(rest( seq )); }Man kann natürlich noch zusätzliche Basisfälle definieren – das kommt auf den Algorithmus an – aber man braucht mindestens einen Basisfall, damit die rekursive Funktion terminiert.´
Rückgabewerte im Basisfall
Oft ist der Basisfall eigentlich der Fall, in dem die Funktion nichts “tun” und der Wert des Ergebnisses vom Basisfall nicht beeinflusst werden soll.
Beispiele:
<T> int length( Seq<T> seq ) { if( isEmpty( seq ) ) return 0; return 1 + length( rest( seq ) ); } // gib jedes 2. Element zurück // wir fangen an bei 0 zu zählen, wie bei Indizes üblich <T> Seq<T> oddElements( Seq<T> seq ) { if( isEmpty( seq ) || isEmpty( rest( seq ) ) ) return emptySeq(); return concat( cons( first( rest( seq ) ) ), oddElements( rest( rest( seq ) ) ) ); } /* Testausgabe: oddElements( cons( 0,1,2,3,4,5 ) ) [1, 3, 5] */Was haben 0 und emptySeq() gemeinsam? Sie beeinflussen den Wert des Ergebnisses nicht.
Würden wir nicht addieren und konkatenieren, sondern im rekursiven Schritt multiplizieren, dann wäre unser Rückgabewert im Basisfall $$1$$.Mathematische Begründung:
Alle Rückgabewerte im Basisfall waren neutrale Elemente ihrer jeweiligen Algebraischen Struktur über der Sorte und dem Operator, auf der im rekursiven Schritt operiert wurde.
In den Beispielen waren dies die Gruppen $$\left( \mathbb{Z}, + \right)$$ und $$\left( \mathrm{Seq}, \circ \right)$$.Hieraus können wir auch noch eine Einsicht gewinnen:
Man kann keinen passenden Rückgabewert finden, der das Ergebnis nicht beeinflusst, wenn man zum Beispiel im rekursiven Schritt mit dem Rückgabewert addiert und multipliziert.Rekursiv Denken
An sich sind wir jetzt mit allem technischen durch – das einzige, das noch fehlt, sind ein paar Anmerkungen, die einem helfen können, rekursive Funktionen zu erstellen. Dies folgt jetzt.
Rekursives Programmieren ist die Mutter aller Divide & Conquer-Strategien: man spaltet das Problem immer wieder in gleichartige Teilprobleme, mit deren Lösung man das ursprüngliche Problem lösen kann, auf, bis man ein “Basisproblem”´ erhält, das leicht zu lösen ist´.
Die meisten Rekursionen, die wir bisher programmiert haben, waren sehr “unbalanciert”:
Bei Sequenzen zum Beispiel teilen wir die Sequenz oft in das erste Element und den Rest auf und bearbeiten dann das Element direkt und lassen in der Rekursion die Funktion das Problem für den Rest der Sequenz lösen und setzen dann alles wieder zusammen – siehe length oder so gut wie alle Funktionen, die wir bisher geschrieben haben.Wenn wir also rekursive Funktionen auf Sequenzen schreiben, müssen wir uns immer überlegen, wie wir mit der Lösung für ein Teilsequenz unserer Eingabesequenz und direktem Zugriff auf ein oder zwei Elemente, die Lösung des Problems für die ganze Sequenz finden.length( cons( "a","b","c","d" ) ) schematisch dargestellt
Dies ist der Grundgedanke der meisten Aufgaben, die wir behandeln.
Hilfsfunktionen
Oft hilft es auch, zusätzliche Hilfsfunktionen zu definieren, die einem die Arbeit erleichtern oder erst möglich machen, wenn die Signatur der Funktion selber nämlich keine Rekursion zulässt.
Als Beispiel die Tower-Funktion´:
// berechnet n^(n^(...)) n-mal Potenzieren (wobei ^ für's Potenzieren steht - deswegen heißt sie Turmfunktion) int tower( int n ) { ensure( n >= 0 ); return _tower( n, n ); } int _tower( int n, int k ) { ensure( k >= 0 ); if( k == 0 ) return 1; return pow( n, _tower( n, k - 1 ) ); } int pow( int a, int n ) { ensure( n >= 0 ); if( n == 0 ) return 1; return a * pow( a, n - 1 ); }Hier brauchen wir einige Hilfsfunktionen, wobei auffallen sollte, dass die eigentliche tower Funktion nur ein Stub (eng. für Stummel) ist und _tower die eigentliche Arbeit erledigt.
Also wenn man nicht wirklich weiter kommt:
Einfach schauen, ob man vielleicht Hilfsfunktionen geschickt benutzen kann.Soweit zur Theorie – im nächsten Post habe ich ziemlich viele Aufgaben gesammelt, die man ohne weiteres lösen kann ´.
Tags: Divide-and-Conquer Strategien, FJava, rekursive Funktionen
![length( [1,2,3,4] ) schematisch dargestellt](http://info1.blackhc.net/wp-content/uploads/2008/11/112808-1421-smartartdep21.png "112808-1421-smartartdep2.png")
