10 Jan 09 Interfaces in 10 Minutes

Ich habe mich heute mal drangehockt und ein kleines Eclipse-Projekt geschrieben, das einerseits versucht Interfaces an Beispielen zu erklären (sehr banale Beispiele, die aber mit vielen Kommentaren versetzt sind), aber auch andererseits zeigt (sozusagen im Fortgeschrittenen-Teil), wie man Klassen definiert, die in For each-Schleifen benutzt werden können, also z.B.:

MeineKlasse meinObject = new MeineKlasse();

// falls die Klasse sich über integer iterieren lässt
for( int i : meinObject ) {
...
}

Es wird als Bonus auch noch gezeigt, wie man auch noch die ersten 10 Fibonacci-Zahlen berechnen könnte 😉

Hier ist das Eclipse-Projekt: Interfaces In 10 Minutes

In der readme.txt steht die empfohlene Reihenfolge, in der man sich die Dateien anschauen sollte.

Für Feedback und Anregungen bin ich wie immer offen
Grüße,
Andreas

Tags: examples, foreach, interface, Java

22 Nov 08 Kontext-freie Grammatiken

Ein paar Worte zu Beginn..

Beim Korrigieren der Hausaufgaben ist mir aufgefallen, dass möglicherweise das Konzept der (kontext-freien) Grammatiken noch nicht zur Ganzheit verstanden wurde, bzw. die Ausdrucksmöglichkeiten noch nicht vollständig erfasst wurden. Natürlich gehört auch Übung und auch ein gewisses Maß an Intuition dazu um “gute” Grammatiken zu schreiben, aber im Folgenden möchte ich versuchen ein paar Hinweise und Tipps zu geben´.

Zuerst möchte ich kurz auf das Konzept von Heuristiken im Software Engineering und in der Informatik allgemein eingehen´:
Heuristiken sind eine Verallgemeinerung von Algorithmen, dadurch gekennzeichnet, dass sie nicht so exakt und präzise formuliert sein müssen wie diese und auch nicht unbedingt immer funktionieren.
Heuristiken sind also “$$\pi$$ mal Daumen”-Ansätze und Regeln um oft gute Lösungen für ein Problem oder ähnliches zu finden, aber auch gleichzeitig Kompromisse.

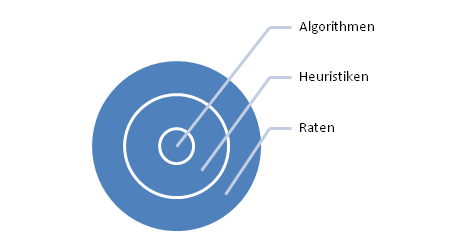
Grammatiken

Betrachten wir nun ein paar “gute” Grammatiken und versuchen daraus Heuristiken abzuleiten.

Als erstes hätten wir die Grammatik aus der Hausaufgabe vom 2. Übungsblatt:

<bool_expr> ::= <bool_term> { “||” <bool_term> }*
<bool_term> ::= <bool_not> { “&&” <bool_not> }*
<bool_not> ::= [ ‘!’ ] <bool_factor>
<bool_factor> ::= <bool_const> | <bool_var> | ‘(‘ <bool_expr> ‘)’
<bool_const> ::= “true” | “false”
<bool_var> ::= ‘X’ | ‘Y’ | ‘Z’

Schon aus dieser Grammatik kann man ein paar Beobachtungen herleiten, die einem helfen zu bestimmen, ob eine Grammatik “gut” ist oder nicht:

• Die Grammatik ist eindeutig, d.h. es gibt nur genau einen Ableitungsbaum für jedes Wort der Sprache, welche die Grammatik darstellt.
• Jeder Operator kommt nur einmal in der Grammatik vor.
• Die Struktur der Grammatik ist einfach (sequentiell) und ähnelt dem Schema des Operatorvorranges´.
• Die geforderte Rekursion tritt nur an einer Stelle auf´.

Die Eindeutigkeit ist besonders wichtig, wenn wir daran denken, für wen solche Grammatiken gemeinhin gedacht sind: Computer/-programme. Programme oder Unterprogramme, die aus einem Ausdruck einen Ableitungsbaum konstruieren, heißen übrigens Parser´.
Eindeutigkeit ist also sicherlich eine Eigenschaft, die wünschenswert ist, wenn wir versuchen einen Ableitungsbaum zu erstellen. Erstellen wir einen Ableitungsbaum müssen wir ja rückwärts vorgehen und versuchen aus den einzelnen Grundelementen, die wir zur Verfügung haben, die Regeln abzuleiten, aus denen sie erzeugt wurden, und aus diesen dann ihre “Elternregeln”, usw. bis wir die Startregel erreichen.

Eindeutigkeit

Wie stellt man nun Eindeutigkeit sicher?

Wir können festlegen:

Zwei fortgeschrittene, verschiedene Ketten von Regelersetzungen (denn Grammatiken definieren ja nichts anderes als Termersetzungen, bei denen auf der rechten Seite immer nur genau ein Nicht-Terminal steht) enden in verschiedenen Wörtern der formalen Sprache (wenn sie überhaupt terminieren)´.

Oder anders gesagt:
Jedes Wort der formalen Sprache besitzt genau einen Ableitungsbaum (Äquivalenz durch Kontraposition).

Die Idee hier ist, dass man Grammatiken nicht nur benutzen kann, um aus vorgegebenen Ausdrücken Ableitungsbäume o.ä. zu konstruieren, sondern auch um neue Ausdrücke zu bauen (wieder analog zu den Konzepten von Termersetzungen, Grundtermen und Normalformen – Quizfrage: was sind hier die Analogien zu Grundformen und Normalformen?).

Als Beispiel (mit der Grammatik aus der Hausaufgabe):

<bool_expr> –> <bool_term> || <bool_term> –> <bool_not> || <bool_term> –> <bool_factor> || <bool_term> –> … –> X | Y

Aber zurück zum Thema: was ist nicht eindeutig?

Betrachten wir:

<startRegel> ::= <regelA> “||” <regelA> | <regelB> “||” <regelB>
.
.
.

Über diese Grammatik können wir keine Aussage bzgl. der Eindeutigkeit machen!
Der Fall, der uns interessiert ist folgender (als Beispiel):

<startRegel> ::= <regelA> | <regelB>
<regelA> ::= <regelC> “||” <regelC>
<regelB> ::= <regelC> “||” <regelC>

Man sieht leicht, dass wir es hier mit einer nicht eindeutigen Grammatik zu tun haben.
Aber genauso wenig eindeutig ist:

<startRegel> ::= <regelA> | <regelB>
<regelA> ::= <regelC> {“||” <regelC>} *
<regelB> ::= <regelC> {“||” <regelC>} +

Oder:

<regelA> ::= <regelA> + <regelA> | <regelA> − <regelA> | <regelA>

(Wieso?)

Worauf ich hinaus will: man kann wohl beliebig komplizierte/nicht-triviale Grammatiken bauen, die nicht eindeutig sind.

Wir kommen also mit dieser Eigenschaft nicht wirklich weiter, außer dass wir sagen können, dass sie wünschenswert ist. Als Heuristik ist sie aber insgesamt tauglich, weil wir sagen können, dass die Eindeutigkeit das große Ziel ist, wonach wir streben, wenn wir Grammatiken schreiben (mit den richtigen Techniken/Vorgehensweisen folgt sie aber fast automatisch).

Das heißt:

Es ist also gut zu versuchen, die Grammatik nicht mehrdeutig werden zu lassen, denn wenn man versucht eindeutige Grammatiken zu schreiben, erhält man automatisch auch einfache/knappe Grammatiken, was auf jeden Fall gut ist.

Semantische Eindeutigkeit

Betrachten wir also nun die 2. Eigenschaft: “Jeder Operator kommt nur einmal vor in der Grammatik vor.”
Die Beobachtung hierbei ist, dass es sinnvoll ist, jeden Operator nur einmal in einer Regel zu beschreiben, denn dann ist klar, dass zumindest dieser Operator eindeutig durch genau eine Regel gematcht (oder von ihr erzeugt) werden kann.

Wir können diese Beobachtung noch allgemeiner fassen, wenn wir uns kurz von dem Beispiel der booleschen Ausdrücke entfernen.

<ifexpr> ::= “if(” <cond> “)” <cmdblock> { “else” <cmdblock> }
<cmdblock> ::= <ifOrCmd> | [ ‘{‘ <ifOrCmd> {<ifOrCmd>}* ‘}’ ]
<ifOrCmd> ::= <command> | <ifexpr>

Hier haben wir es nicht mehr wirklich mit Operatoren zu tun, dafür aber mit if-Anweisungen. Man kann aber auch hier etwas feststellen:
jede Regel behandelt genau ein semantisches Konzept´.

Die Bezeichnung “semantisches Konzept” versucht auszudrücken, dass es sich um ein abstraktes Konzept handelt, das Teil der Sprache ist, und dass wir die Konzepte nach ihrer Semantik, also ihrer Bedeutung, unterscheiden.
Diese Feinheit ist insbesondere dann wichtig, wenn wir Sprachen betrachten, bei denen verschiedene Konzepte mit unterschiedlicher Bedeutung die gleiche Syntax haben.
Das ist jetzt nicht an den Haaren herbeigezogen, sondern es gibt sogar sehr viele Programmiersprachen, bei denen diese Unterscheidung wichtig ist. Als Beispiel sei hier nur Visual Basic angegeben.

In Visual Basic wird Variablen mit = ein Wert zugewiesen, andererseits wird in Bedingungen auch mit = überprüft, ob zwei Variablen den gleichen Wert haben. Natürlich ist es dann auch wahrscheinlich, dass es Probleme mit der Eindeutigkeit gibt; diese werden aber durch geschickte Wahl der Regeln oder Kontextbedingungen (siehe Vorlesung) umgangen.

Als Gegenbeispiel, dass diese Eigenschaft nicht immer erfüllt ist, betrachten wir dazu einmal einen Ausschnitt der Sprache Java aus den offiziellen Spezifikationen:

IfThenStatement:
if ( Expression ) Statement

IfThenElseStatement:
if ( Expression ) StatementNoShortIf else Statement

IfThenElseStatementNoShortIf:
if ( Expression ) StatementNoShortIf else StatementNoShortIf

Expression:
“ein boolescher Ausdruck”

Statement:
“eine beliebige weitere Anweisung (auch IfThenStatement und IfThenElseStatement)”

StatementNoShortIf:
“eine beliebige weitere Anweisung (aber nur IfThenElseStatementNoShortIf und nicht IfThenStatement oder IfThenElseStatement)”

Ohne weiter auf den tieferliegenden Grund einzugehen (näheres dazu findet sich in den Spezifikationen) kann man aber feststellen, dass hier ein semantisches Konzept – die if-else-Anweisung – in mehr als einer Regel behandelt wird. D.h. die Beobachtung über die semantischen Konzepte ist auch höchstens eine Heuristik um eine gute Grammatik zu konstruieren und man muss auch daran denken, dass die Unterteilung nicht immer ganz klar ist.

Als Beleg dafür, dass sie trotzdem eine sehr nützliche Heuristik ist, sei auf die Übung 3 im 2. Übungsblatt verwiesen:

<table> ::= “<table” {<border>} “>” <headerRow> {<rows>}* “</table>”
<border> ::= “border=\”” <number> “\””
<headerRow> ::= “<tr>” {<headerData>}* “</tr>”
<headerData> ::= “<th>” <data> “</th>”
<rows> ::= “<tr>” {<rowData>}* “</tr>”
<rowData> ::= “<td>” <data> “</td>”
<data> ::= <table> | <number> | <text>
<number> ::= [ <ziffer> {<ziffer> | ‘0’}* ] | ‘0’
<ziffer> ::= ‘1’ | ‘2’ | ‘3’ | ‘4’ | ‘5’ | ‘6’ | ‘7’ | ‘8’ | ‘9’
<text> ::= {‘a’ | ‘b’ | ‘c’ | … | ‘z’ | ‘A’ | ‘B’ | … | ‘Z’}+

Struktur der Grammatik

Aus den bisher angegebenen Grammatiken kann man auch noch zwei weitere wichtige Heuristiken herleiten. Vorher schauen wir uns aber zuerst noch die 3. Eigenschaft vom Anfang an: “Die Struktur der Grammatik ist einfach (sequentiell) und ähnelt dem Schema des Operatorvorrang.”

Zuerst einmal: was ist damit gemeint?

Beide Teilaussagen der Eigenschaft werden hoffentlich klar(er), wenn man folgende Hierarchie anschaut:

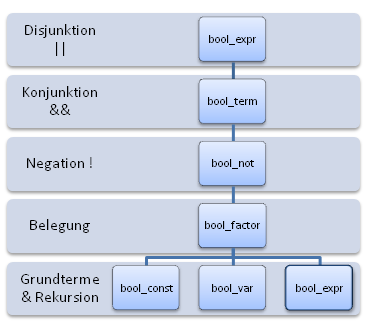
Erinnern wir uns jetzt, dass bei der Aufgabe folgender Operatorvorrang gelten soll (vom schwächeren zum stärker bindenden Operator hin):

Dann ist klar, dass Operatorvorrang und Regelhierarchie übereinstimmen und dies ist auch allgemein so:

Damit kann man schon recht leicht “nach Schema F” beliebige Rechenstrukturen mit beliebigen Operatorpräzedenzen/-vorrang abarbeiten und in eine Grammatik umwandeln, es stellt sich nur die Frage, wie es bei anderen Sprachkonstrukten aussieht.

Auf jeden Fall können wir noch ein anderes Ergebnis zusammenfassen, das bisher in allen Lösungen und Beispiele sichtbar war und auch so in der 3. Eigenschaft formuliert ist:

Es ist also sinnvoll, dass wir immer versuchen, die Regeln so einfach wie möglich zu formulieren, weil dies bei den Sprachen, die man normalerweise behandelt auch möglich ist. (Entweder das, oder es gibt gar keine Darstellung der Sprache als kontext-freie Grammatik – siehe dazu die Aufgabe 4 des 2. Übungsblattes mit der Frage, ob es eine BNF-Beschreibung der Sprache $$a^nb^nc^n$$ gibt.)

Insbesondere gibt uns das auch noch einen Hinweis, wie weit man die semantischen Konzepte versucht zu vereinfachen und zwar: so weit wie möglich. D.h. lieber mehr einfach strukturierte Regeln als eine äußerst komplexe.

Rekursion

Als letztes noch die 4. Beobachtung: “Die geforderte Rekursion tritt nur an einer Stelle auf.”. Aus den Beispielen kann man sehen, dass die Rekursion meistens erst sehr weit “unten” in der Hierarchie auftritt.
Dadurch, dass man die Rekursion möglichst weit nach unten “drückt”, also in die Richtung der Grundterme hin, kann man leicht sicherstellen, dass die Rekursion möglichst allgemein gilt und gleichzeitig erübrigt sich dadurch eine weitere Behandlung der gleichen Rekursion in der Hierarchie darüber.

In der Vorlesung wurde auch noch erwähnt, dass sich kontext-freie Grammatiken besonders zur Darstellung von Klammerstrukturen eignen, indem man rekursive Regeln aufstellt. Die Grammatiken der Tabellen und auch die geklammerten booleschen Ausdrücke oben sind gute Beispiele dafür und auch für das “Herunterdrücken” des Rekursionsfalles.

Hierzu noch ein kleines Beispiel für eine Grammatik, die alle gültigen Datensorten in FJava beschreibt:

<BasisTyp> ::= “int” | “float” | …

<WrapperTyp> ::= “Integer” | “Float” | …
<SequenzTyp> ::= “Seq” “<” <ObjektTyp> “>”

<ObjektTyp> ::= <WrapperTyp> | <SequenzTyp>

<Typ> ::= <BasisTyp> | <ObjektTyp>

Wir fassen also zusammen:

Zusammenfassung und Ausblick

Damit haben wir fünf Heuristiken kennengelernt, die einem helfen können, bessere Grammatiken zu schreiben:

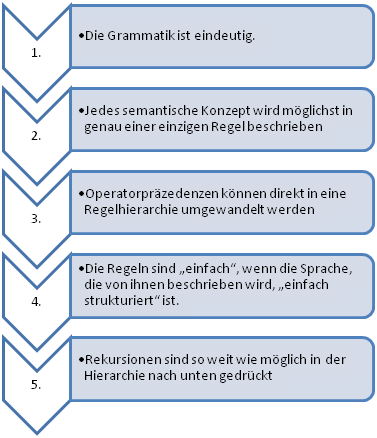
Zum Abschluss noch zwei zusätzliche Tipps, um sicherer im Umgang mit kontext-freien Grammatiken zu werden:

• Üben, üben, üben!
  Wir haben Fjava in der Vorlesung nicht wirklich definiert, deswegen bietet es sich an für die Sprache selbst eine Grammatik zu entwerfen.
  Es gibt aber auch Tools frei im Internet, mit denen man Parser aus einer BNF-ähnlichen Beschreibung einer Sprache erstellen kann. Es wäre also möglich die “Broy-Notation” aus der Vorlesung in Fjava umzuwandeln (mittels eines solchen Parsers und einfachen Textersetzungen). Wenn es dazu Fragen gibt, dann kann ich da gerne ein paar Links heraussuchen.
• Es gibt viele Programmiersprachen und jede etwas ernsthaftere hat eine Spezifikation und alle beschreiben ihre Sprachen mittels einer Notation, die mehr oder weniger direkt auf der BNF-Notation basiert – man kann dort auch nach Inspirationen suchen 😉

Falls es noch Fragen gibt oder Feedback, dann schreibt mir eine Email oder nutzt die Kommentarfunktion ´

Tags: BNF, Grammatik, Heuristik, Java